(1)偏差函数构造
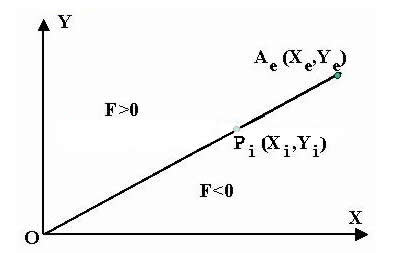
对于第一象限直线OA上任一点(X,Y):X/Y = Xe/Ye
若刀具加工点为Pi(Xi,Yi),则该点的偏差函数Fi可表示为
若Fi= 0,表示加工点位于直线上;
若Fi> 0,表示加工点位于直线上方;
若Fi< 0,表示加工点位于直线下方。
(2)偏差函数字的递推计算
采用偏差函数的递推式(迭代式)
既由前一点计算后一点
Fi =Yi Xe -XiYe
若Fi>=0,规定向 +X 方向走一步
Xi+1 = Xi +1
Fi+1 = XeYi –Ye(Xi +1)=Fi –Ye
若Fi<0,规定 +Y 方向走一步,则有
Yi+1 = Yi +1
Fi+1 = Xe(Yi +1)-YeXi =Fi +Xe
(3)终点判别
直线插补的终点判别可采用三种方法。
1)判断插补或进给的总步数:;
2)分别判断各坐标轴的进给步数;
3)仅判断进给步数较多的坐标轴的进给步数。
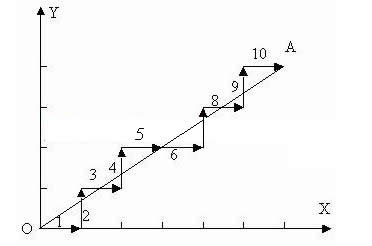
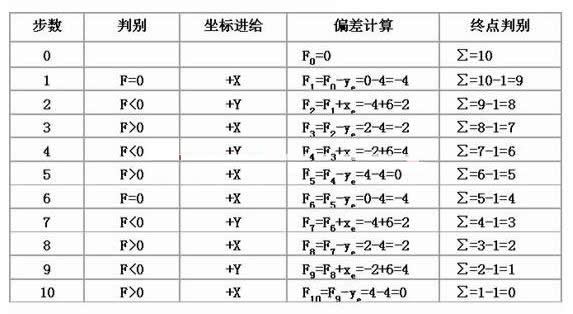
(4)逐点比较法直线插补举例
对于第一象限直线OA,终点坐标Xe=6 ,Ye=4,插补从直线起点O开始,故F0=0 。终点判别是判断进给总步数N=6+4=10,将其存入终点判别计数器中,每进给一步减1,若N=0,则停止插补。