使用DDA法插补时，其插补进给速度v不仅与系统的迭代频率V（即脉冲源频率）成正比，而且还与余数寄存器的容量N成反比，与直线段的长度 L（或圆弧半径 R）成正比。它们之间有下述关系成立：
（2-12）
式中 v——插补进给速度；
——系统脉冲当量；
L ——直线段的长度；
N——寄存器的容量；
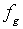——迭代频率。
显然，即使编制同样大小的速度指令，但针对不同长度的直线段，其进给速度是变化的（假设 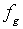和 N为固定），必须设法加以改善。常用的改善方法是左移规格化和进给速率编程（FRN）。
由上面DDA圆弧插补例子可以看出，当插补第Ⅰ象限逆圆时， y坐标率先到达。这时若不强制 y方向停止迭代，将会出现超差，不能到达正确的终点。为了改善这一情况，常用余数寄存器预置数的办法来解决。
以下就来讨论使DDA法从原理走向实用必须解决的速度和精度控制问题。
1．进给速度的均匀化措施——左移规格化
从上述可知，数字积分器溢出脉冲的频率与被积函数寄存器中的存数成正比。如用DDA作直线插补时，每个程序段的时间间隔是固定不变的，因为不论加工行程长短，都必须同样完成
次的累加运算。就是说行程长，走刀快；行程短，走刀慢。所以各程序段的进给速度是不一致的。这样影响了加工的表面质量，特别是行程短的程序段生产率低。为了克服这一缺点，使溢出脉冲均匀，溢出速度提高，通常采用左移规格化处理。
所谓“左移规格化”处理，是当被积函数的值比较小时，如被积函数寄存器有 
个前零时，若直接迭代，那么至少需要2i次迭代，才能输出一个溢出脉冲，致使输出脉冲的速率下降。因此在实际的数字积分器中，需把被积函数寄存器中的前零移去即对被积函数实现“左移规格化”处理。经过左移规格化的数就成为规格化数——寄存器中的数其最高位为“1”时，该数即称为规格化数；反之最高位为“0”的数称为非规格化数。显然，规格化数累加两次必有一次溢出，而非规格化数必须作两次以上或多次累加才有一次溢出。
2．提高插补精度的措施——余数寄存器预置数
前已述及，DDA直线插补的插补误差小于一个脉冲当量，但是DDA圆弧插补的插补误差有可能大于一个脉冲当量，其原因是这样的：由于数字积分器溢出脉冲的频率与被积函数寄存器的存数成正比，当在坐标轴附近进行插补时，一个积分器的被积函数值接近于零，而另一个积分器的被积函数值却接近最大值（圆弧半径），这样，后者可能连续溢出，而前者几乎没有溢出，两个积分器的溢出脉冲速率相差很大，致使插补轨迹偏离理论曲线（见图2—5）。
为了减小插补误差，提高插补精度，可以把积分器的位数增多，从而增加迭代次数。这相当于把图2—7矩形积分的小区间Δt取得更小。这样做可以减小插补误差，但是进给速度却降低了，所以我们不能无限制地增加寄存器的位数。在实际的积分器中，常常应用一种简便而行之有效的方法——余数寄存器预置数。即在DDA插补之前，余数寄存器JRx和JRy预置某一数值（不是零），这一数值可以是最大容量，即2n-1，也可以是小于最大容量的某一个数，如2n/2，常用的则是预置最大容量值（称为置满数或全加载）和预置0.5（称为半加载）两种。
“半加载”是在DDA迭代前，余数寄存器JRx和JRy的初值不是置零，而是置1000…000（即0.5），也就是说，把余数寄存器JRx和JRy的最高有效位置“1”，其余各位均置“0”，这样，只要再叠加0.5，余数寄存器就可以产生第一个溢出脉冲，使积分器提前溢出。这在被积函数较小，迟迟不能产生溢出的情况时，有很大的实际意义，因为它改善了溢出脉冲的时间分布，减小了插补误差。
“半加载”可以使直线插补的误差减小到半个脉冲当量以内，一个显而易见的例子是：若直线OA的起点为坐标原点，终点坐标是A（15，1），没有“半加载”时，x积分器除第一次迭代没有溢出外，其余15次迭代均有溢出；而y积分器只有在第16次迭代时才有溢出脉冲（见图2—17（a））。若进行了“半加载”，则x积分器除第9次迭代没有溢出外，其余15次均有溢出；而y积分器的溢出提前到第8次迭代有溢出，这就改善了溢出脉冲的时间分布，提高了插补精度（见图2—17（a））。
图2-17 “半加载”后的轨迹
“半加载”使圆弧插补的精度得到明显改善。若对图2—17（b）的例子进行“半加载”，其插补轨迹如图中的折线所示，插补过程见表2—7。仔细比较后可以发现，“半加载”使x积分器的溢出脉冲提前了，从而提高了插补精度。
所谓“全加载”，是在DDA迭代前将余数寄存器JRx 和JRy的初值置成该寄存器的最大容量值（当为n位时，即置入2n-1），这会使得被积函数值很小的坐标积分器提早产生溢出，插补精度得到明显改善。
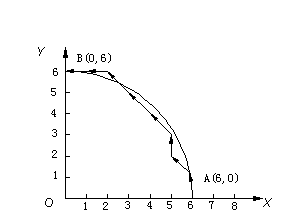
图2-18 “全加载”后的实际轨迹
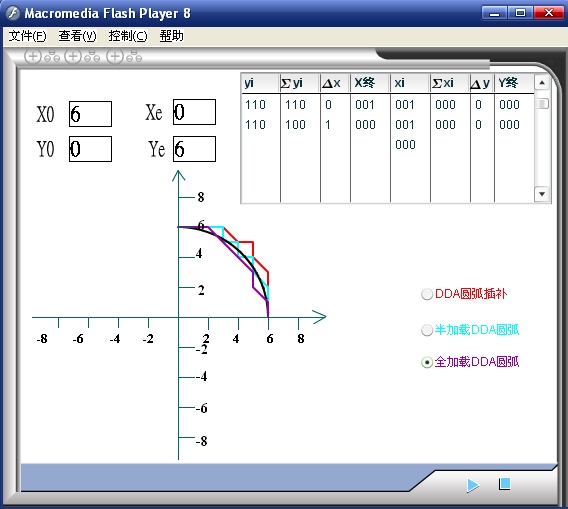
图2—18是使用“全加载”的方法得到的插补轨迹，由于被积函数寄存器和余数寄存器均为三位，置入最大数为7（111）。
