设我们要对 xy平面上的直线进行脉冲分配，直线起点为坐标原点 O，终点为 E(xe,ye)，如图2-8所示。
图2-8 合成速度与分速度的关系
假定 vx和 vy分别表示动点在 x和 y方向的移动速度，则在 x和 y方向上的移动距离微小增量 Δx和 Δy应为
（2—5）
对直线函数来说， vx和 vy是常数，则下式成立：
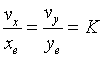（2—6）
式中K为比例系数。
在Δt时间内，x和y位移增量的参数方程为
（2—7）
动点从原点走向终点的过程，可以看作是各坐标每经过一个单位时间间隔Δt分别以增量 Kxe和 Kye同时累加的结果。经过m次累加后，x和y分别都到达终点 E(xe,ye)，即下式成立：
（2—8）
则
或
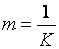（2—9）
上式表明，比例系数K和累加次数 
的关系是互为倒数。因为m必须是整数，所以 K一定是小数。在选取K时主要考虑每次增量 Δx或 Δy不大于1，以保证坐标轴上每次分配进给脉冲不超过一个单位步距，即
Δx= Kxe<1
Δy= Kye<1
式中 xe和 ye的最大容许值受控制机的位数及用几个字节存储坐标值所限制。如用TP801（Z80）单板机作控制机，用两个字节存储坐标值，因该单板机为8位机，故 xe和 ye的最大容许寄存容量为216-1=65 535。为满足 Kxe<1及 Kye<1的条件，即
Kxe= K（216-1）<1
Kye= K（216-1）<1
则
如果取
，则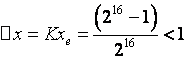
，即满足 Kxe<1的条件。这时累加次数为
次
一般情况下，若假定寄存器是n位，则 xe和 ye的最大允许寄存容量应为2n-1（各位全1时），若取
则
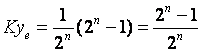
显然，由上式决定的Kxe和Kye是小于1的，这样，不仅决定了系数
，而且保证了Δx和Δy小于1的条件。因此，刀具从原点到达终点的累加次数m就有
当时，对二进制数来说， Kxe与 xe的差别只在于小数点的位置不同，将 xe的小数点左移n位即为 Kxe。因此在n位的内存中存放 xe（ xe为整数）和存放 Kxe的数字是相同的，只是认为后者的小数点出现在最高位数n的前面。
当用软件来实现数字积分法直线插补时，只要在内存中设定几个单元，分别用于存放 xe及其累加值∑xe和 ye及其累加值∑ye。将∑xe和∑ye赋一初始值，在每次插补循环过程中，进行以下求和运算：
∑xe+xe→ ∑xe
∑ye+ye→ ∑ye
将运算结果的溢出脉冲Δx和Δy用来控制机床进给，就可走出所需的直线轨迹。
综上所述，可以得到下述结论：
数字积分法插补器的关键部件是累加器和被积函数寄存器，每一个坐标方向就需要一个累加器和一个被积函数寄存器。一般情况下，插补开始前，累加器清零，被积函数寄存器分别寄存 xe和 ye；插补开始后，每来一个累加脉冲Δt，被积函数寄存器里的内容在相应的累加器中相加一次，相加后的溢出作为驱动相应坐标轴的进给脉冲 Δx（或 Δy），而余数仍寄存在累加器中；当脉冲源发出的累加脉冲数m恰好等于被积函数寄存器的容量2n时，溢出的脉冲数等于以脉冲当量为最小单位的终点坐标，刀具运行到终点。
数字积分法插补第Ⅰ象限直线的程序流程图如图2-11所示。
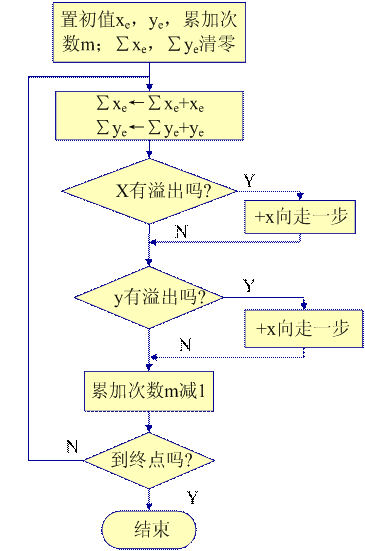
图2-11 DDA直线插补流程图
下面举例说明DDA直线插补过程。设要插补图2—12所示的直线轨迹OA，起点坐标为 O（0，0），终点坐标为 A（7，10）。若被积函数寄存器Jvx和Jvy，余数寄存器 JRx和JRy，以及终点减法计数器JE均为四位二进制寄存器，则迭代次数为m=24=16次时插补完成。在插补前，JE，JRx，JRy均为零，Jvx和Jvy分别存放 xe=7（即二进制的0111）， ye=10（即二进制的1010）。在直线插补过程中Jvx和Jvy中的数值始终为xe 和ye 保持不变。本例的具体轨迹如图2-12中的折线所示，由此可见，经过16次迭代之后， x和 y坐标分别有7个和10个脉冲输出。直线插补轨迹与理论曲线的最大误差不超过1个脉冲当量。
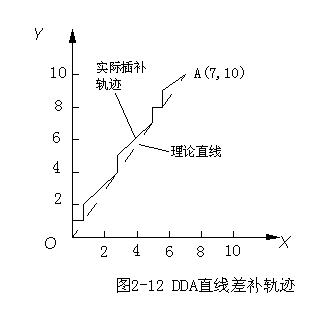
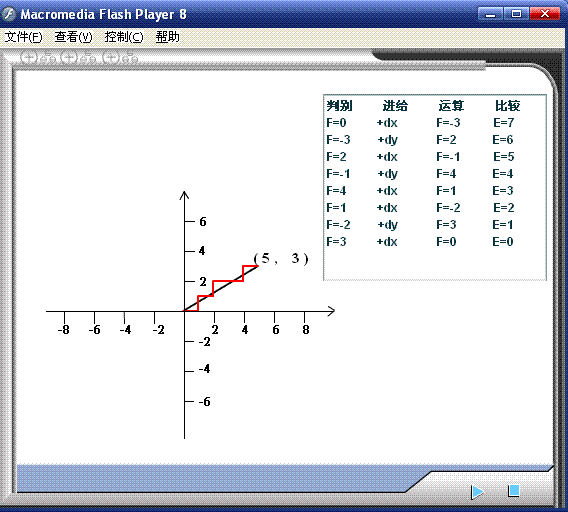
图2-13 DDA直线插补过程
