由高等数学可知,求函数y =f(t)对t的积分运算,从几何概念上讲,就是求此函数曲线 所包围的面积 F(图2—7),即


若把自变量的积分区间[a,b]等分成许多有限的小区间![]() (其中
(其中 ![]() ),这样,求面积可以转化成求有限个小区间面积之和,即
),这样,求面积可以转化成求有限个小区间面积之和,即

数字运算时,Δt一般取最小单位“1”,即一个脉冲当量,则
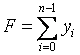
由此可见,函数的积分运算变成了变量的求和运算。当所选取的积分间隔Δt足够小时,
则用求和运算代替求积运算所引起的误差可以不超过允许的值。
由高等数学可知,求函数y =f(t)对t的积分运算,从几何概念上讲,就是求此函数曲线 所包围的面积 F(图2—7),即


若把自变量的积分区间[a,b]等分成许多有限的小区间![]() (其中
(其中 ![]() ),这样,求面积可以转化成求有限个小区间面积之和,即
),这样,求面积可以转化成求有限个小区间面积之和,即

数字运算时,Δt一般取最小单位“1”,即一个脉冲当量,则
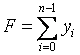
由此可见,函数的积分运算变成了变量的求和运算。当所选取的积分间隔Δt足够小时,
则用求和运算代替求积运算所引起的误差可以不超过允许的值。
2023-05-30511
2023-05-30595
2023-05-30574
2023-05-30587
2023-05-30569
2023-05-30634
2023-05-30467
2023-05-30578
2023-05-30444
2023-05-30498