图2-31所示为第Ⅰ象限顺圆弧段![]() ,圆弧方程为
,圆弧方程为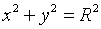
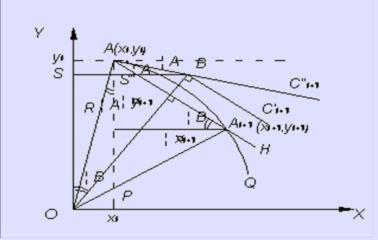
图3-31 扩展DAA圆弧插补
设现时刀具处在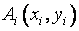 点的位置。若在一个采样周期
点的位置。若在一个采样周期![]() 内,刀具沿切线方向的轮廓进给步长为
内,刀具沿切线方向的轮廓进给步长为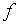 ,即进给一步后应到达
,即进给一步后应到达![]() 点,显然,
点,显然,![]() 的长度为
的长度为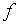 。由图可见,它的径向误差是较大的。扩展DDA算法并不是让刀具沿切线进给,而是将切线逼近圆弧的方法转化为弦线逼近法。
。由图可见,它的径向误差是较大的。扩展DDA算法并不是让刀具沿切线进给,而是将切线逼近圆弧的方法转化为弦线逼近法。
如果我们通过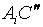 线段的中点
线段的中点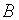 作半径为
作半径为![]() 的圆弧的切线
的圆弧的切线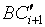 ,再通过
,再通过![]() 点作
点作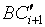 的平行线
的平行线![]() ,即
,即![]() ∥
∥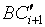 ,并在
,并在![]() 上截取
上截取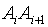 =
=![]() =
=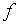 (容易证明
(容易证明![]() 点必不在圆弧侧)。扩展DDA就是用线段
点必不在圆弧侧)。扩展DDA就是用线段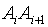 进给来代替
进给来代替![]() 的切线段进给,即扩展DDA在一个采样周期内计算的结果,应是刀具从
的切线段进给,即扩展DDA在一个采样周期内计算的结果,应是刀具从![]() 点沿弦线走到
点沿弦线走到![]() 点(而不是沿切线走到
点(而不是沿切线走到![]() 点)。显然,这样进给使径向误差减小了。
点)。显然,这样进给使径向误差减小了。
现在我们就来计算在采样周期![]() 内的轮廓进给步长
内的轮廓进给步长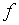 之坐标分量
之坐标分量![]() 和
和![]() 值,得到了此两值,就很容易得到本次采样周期后应达到的坐标位置
值,得到了此两值,就很容易得到本次采样周期后应达到的坐标位置![]() 。
。

设刀具以恒速进给,即在每个采样周期![]() 内的进给速度均为
内的进给速度均为![]() ,显然,
,显然,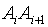 =
=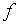 =
=![]() 。过
。过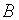 点作
点作![]() 轴的平行线
轴的平行线![]() 交
交![]() 轴于
轴于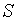 点,交
点,交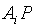 线段于
线段于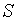 点。可以看出,直角△
点。可以看出,直角△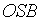 与直角△
与直角△![]() 相似,从而有比例关系:
相似,从而有比例关系:
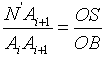 (2-34)
(2-34)
式中 ![]() =
=![]() ;
; ![]()
在直角△ 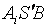 中
中
![]()
因此
![]()
在直角△ ![]() 中
中
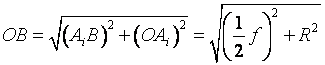
将以上各式代入式(2-34),有
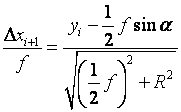
将式(2-32)代入上式并整理,得
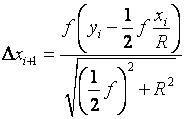
因为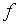
![]() ,故将
,故将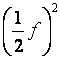 略去不计,则上式为
略去不计,则上式为
若令
![]()
则
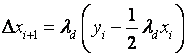 (2-35)
(2-35)
在上述两相似三角形的关系中,还有下式成立:
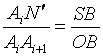
即
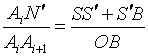
已知
![]()
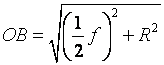
由直角△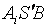 得
得
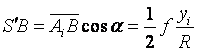
而![]() =
=![]() ,因此
,因此
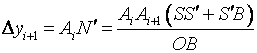 =
=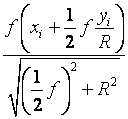
同理,因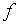
![]() ,故略去
,故略去 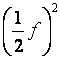 不计,则
不计,则
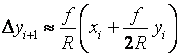
仍记
![]()
则
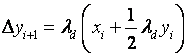 (2-36)
(2-36)
由于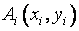 为已知,故利用式(2-35)和(2-36)很容易求得
为已知,故利用式(2-35)和(2-36)很容易求得![]() 和
和![]() 值。有了此两值,就可算出本次采样周期刀具应达到的坐标位置
值。有了此两值,就可算出本次采样周期刀具应达到的坐标位置![]() 和
和![]() 值,即
值,即
![]()
![]()
依照此原理,读者不难得出其他象限及其他走向的圆弧插补之计算公式。


