采用时间分割插补进行圆弧插补的基本方法是内接弦线逼近圆弧。只要根据半径合理选用进给速度F，可使逼近精度满足要求。
将插补计算坐标系的原点选在被插补圆弧的圆心上，以第一象限顺圆为例，讨论圆弧插补原理。
P（Xi，Yi）为圆上某一插补点A，P（Xi+1，Y i+1）为下一插补C，直线段AC（=ΔL）为本次的合成进给量，D为AC的中点，为本次插补的逼近误差δ。由几何关系可得：
ΔABC∽ΔODym
那么有 γi=α+Δαi/2
则有 cosγi =cos（α+Δαi/2）=ym/（R-δ）=（yi-Δyi /2）/（R-δ）
由于Δyi和δ未知，故进行如下近似处理：
由于ΔL很小，可用Δi-1替代Δyi；由于R>>δ，可用R替代R-δ。因此有：
cosγi =（yi-Δyi-1 /2）/R 起点的Δy0采用DDA法求得：Δy0=ΔL y0/R。
算法（1）和（2）如何用，可作与直线插补类似的分析，结论为：先计算大的坐标增量，后计算小的坐标增量。
同样，引入引导坐标的概念，可将考虑顺逆和不同象限的16组插补计算公式归结为两组：
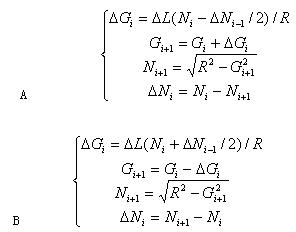
顺圆插补和逆圆插补在各象限采用公式的情况。
在插补公式的推导中，采用了近似计算，cosγi值必然产生偏差，求得的插补值会有误差，这个误差：对轨迹精度来说，由于算法中采用公式 
，插补点（ 
）总可以保证在圆上，故对轨迹精度没有影响。
会导致合成进给量的波动，引起速度不均匀；对逼近误差有影响，当实际γi小于准确γi时，逼近误差比给定的大。但波动的不均匀系数最大：λmax<0.35%，影响是很小的。
