如上所述,偏差计算是逐点比较法关键的一步。下面以第Ⅰ象限直线为例导出其偏差计算公式。
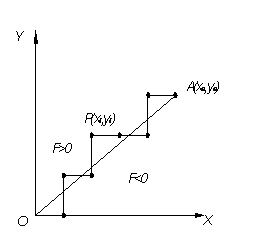
图2-1 直线插补过程
如图2—1所示,假定直线![]() 的起点为坐标原点,终点A的坐标为
的起点为坐标原点,终点A的坐标为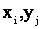 为加工点,若P点正好处在直线
为加工点,若P点正好处在直线![]() 上,那么下式成立:
上,那么下式成立:
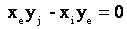
若任意点![]() 在直线
在直线![]() 的上方(严格地说,在直线
的上方(严格地说,在直线![]() 与y轴所成夹角区域内),那么有下述关系成立:
与y轴所成夹角区域内),那么有下述关系成立:
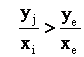
亦即: ![]()
由此可以取偏差判别函数![]() 为:
为:
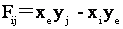
由![]() 的数值(称为“偏差”)就可以判别出P点与直线的相对位置。即:
的数值(称为“偏差”)就可以判别出P点与直线的相对位置。即:
当![]() =0时,点
=0时,点![]() 正好落在直线上;
正好落在直线上;
当![]() >0时,点
>0时,点![]() 落在直线的上方;
落在直线的上方;
当![]() <0时,点
<0时,点![]() 落在直线的下方。
落在直线的下方。
从图2—1看出,对于起点在原点,终点为A(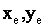 )的第Ⅰ象限直线OA来说,当点P在直线上方(即
)的第Ⅰ象限直线OA来说,当点P在直线上方(即![]() >0)时,应该向+x方向发一个脉冲,使机床刀具向+x方向前进一步,以接近该直线;当点P在直线下方(即
>0)时,应该向+x方向发一个脉冲,使机床刀具向+x方向前进一步,以接近该直线;当点P在直线下方(即![]() <0)时,应该向+y方向发一个脉冲,使机床刀具向+y方向前进一步,趋向该直线;当点P正好在直线上(即
<0)时,应该向+y方向发一个脉冲,使机床刀具向+y方向前进一步,趋向该直线;当点P正好在直线上(即![]() =0)时,既可向+x方向发一脉冲,也可向+y方向发一脉冲。因此通常将
=0)时,既可向+x方向发一脉冲,也可向+y方向发一脉冲。因此通常将![]() >0和
>0和![]() =0归于一类,即
=0归于一类,即![]() ≥0。这样从坐标原点开始,走一步,算一次,判别
≥0。这样从坐标原点开始,走一步,算一次,判别![]() ,再趋向直线,逐点接近直线
,再趋向直线,逐点接近直线![]() ,步步前进。当两个方向所走的步数和终点坐标A(
,步步前进。当两个方向所走的步数和终点坐标A(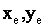 )值相等时,发出终点到达信号,停止插补。
)值相等时,发出终点到达信号,停止插补。
对于图2—1的加工直线OA,我们运用上述法则,根据偏差判别函数值,就可以获得如图中折线段那样的近似直线。
但是按照上述法则进行![]() 的运算时,要作乘法和减法运算,这对于计算过程以及具体电路实现起来都不很方便。对于计算机而言,这样会影响速度;对于专用控制机而言,会增加硬件设备。因此应简化运算,通常采用的是迭代法,或称递推法,即每走一步后新加工点的加工偏差值用前一点的加工偏差递推出来。下面推导该递推式:
的运算时,要作乘法和减法运算,这对于计算过程以及具体电路实现起来都不很方便。对于计算机而言,这样会影响速度;对于专用控制机而言,会增加硬件设备。因此应简化运算,通常采用的是迭代法,或称递推法,即每走一步后新加工点的加工偏差值用前一点的加工偏差递推出来。下面推导该递推式:
已经知道,加工点的坐标为(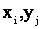 )时的偏差为:
)时的偏差为:
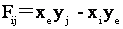
若![]() ≥0时,则向x轴发出一进给脉冲,刀具从这点即(
≥0时,则向x轴发出一进给脉冲,刀具从这点即(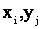 )点向x方向前进一步,到达新加工点P(
)点向x方向前进一步,到达新加工点P(![]() ),
),
![]() ,因此新加工点P(
,因此新加工点P(![]() )的偏差值为
)的偏差值为
![]()
即: ![]() (2-1)
(2-1)
如果某一时刻,加工点P( 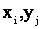 )的
)的 ![]() <0,则向y轴发出一个进给脉冲,刀具从这一点向y方向前进一步,
<0,则向y轴发出一个进给脉冲,刀具从这一点向y方向前进一步,
新加工点P(![]() )的偏差值为
)的偏差值为
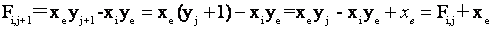
即:
![]() (2-2)
(2-2)
根据式(2—1)及式(2—2)可以看出,新加工点的偏差完全可以用前一加工点的偏差递推出来。
综上所述,逐点比较法的直线插补过程为每走一步要进行以下4个节拍(步骤),即判别、进给、运算、比较。
(1) 判别。根据偏差值确定刀具位置是在直线的上方(或线上),还是在直线的下方。
(2) 进给。根据判别的结果,决定控制哪个坐标(x或y)移动一步。
(3) 运算。计算出刀具移动后的新偏差,提供给下一步作判别依据。根据式(2—1)及式(2—2)来计算新加工点的偏差,使运算大大简化。但是每一新加工点的偏差是由前一点偏差![]() 推算出来的,并且一直递推下去,这样就要知道开始加工时那一点的偏差是多少。当开始加工时,我们是以人工方式将刀具移到加工起点,即所谓“对刀”,这一点当然没有偏差,所以开始加工点的
推算出来的,并且一直递推下去,这样就要知道开始加工时那一点的偏差是多少。当开始加工时,我们是以人工方式将刀具移到加工起点,即所谓“对刀”,这一点当然没有偏差,所以开始加工点的![]() =0。
=0。
(4) 比较。在计算偏差的同时,还要进行一次终点比较,以确定是否到达了终点。若已经到达,就不再进行运算,并发出停机或转换新程序段的信号。
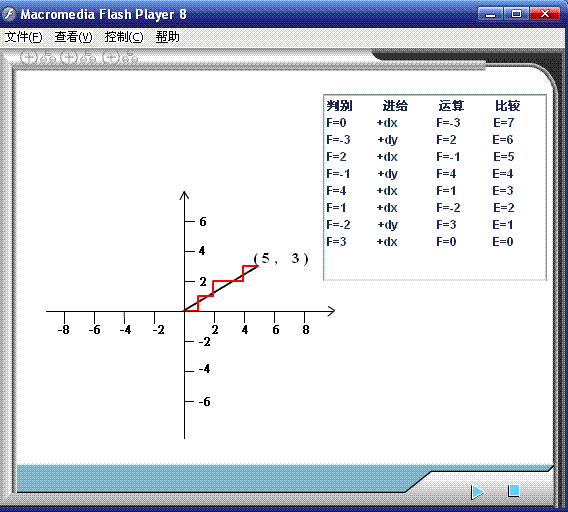
下面以实例来验证图2—1。设欲加工直线OA,其终点坐标为![]() =5*,
=5*,![]() =3*,则终点判别值可取为
=3*,则终点判别值可取为![]() (终点判别方法详见下述)。开始时偏差
(终点判别方法详见下述)。开始时偏差![]() ,加工过程的运算节拍如表2—1所示。
,加工过程的运算节拍如表2—1所示。
图2-2 逐点比较法直线插补过程
表2-1 逐点比较法直线插补运算举例
| 序号 | 工作节拍 | |||
| 第1拍:判别 | 第2拍:进给 | 第3拍:运算 | 第4拍:比较 | |
| 1 | F00=0 | +∆x | F10= F00-ye=0-3= -3 | E7= E8-1=7 |
| 2 | F10(= -3)<0 | +∆y | F11 = F10+xe= -3+5=2 | E6= E7-1=6 |
| 3 | F11(= 2)>0 | +∆x | F21= F11-ye=2-3= -1 | E5= E6-1=5 |
| 4 | F21(= -1)<0 | +∆y | F22= F21+xe= -1+5=4 | E4= E5-1=4 |
| 5 | F22(= 4)>0 | +∆x | F32= F22-ye=4-3= 1 | E3= E4-1=3 |
| 6 | F32(= 1)>0 | +∆x | F42 = F32-ye=1-3= -2 | E2= E3-1=2 |
| 7 | F42(= -2)<0 | +∆y | F43= F42+xe= -2+5=3 | E1=E2-1=1 |
| 8 | F43(= 3)>0 | +∆x | F53= F43-ye=3-3=0 | E0=E1-1=0 |
| 到达终点 | ||||