
在上图,沿直线OA伸长(亦可缩短,图中未示出)一个刀具半径r后,![]() 点的坐标是
点的坐标是
![]()
![]()
式中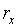 和
和 ![]() 是刀具半径偏移量
是刀具半径偏移量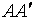 (=r)在x和y轴上的分量。
(=r)在x和y轴上的分量。
在普通NC系统中,当读带机读入![]() 和
和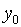 后分别存放在
后分别存放在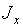 和
和![]() 中,然后计算装置在不输出进给脉冲的情况下(即工作台不动),作直线插补运算。此时,
中,然后计算装置在不输出进给脉冲的情况下(即工作台不动),作直线插补运算。此时,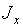 和
和![]() 的数相当于直线插补时的终点坐标,所以在插补过程中
的数相当于直线插补时的终点坐标,所以在插补过程中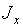 和
和![]() 的内容是不变的。
的内容是不变的。
另外再用两条寄存器![]() 及
及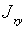 分别记取在直线
分别记取在直线![]() 插补的过程中x轴和y轴的输出插补脉冲(此脉冲不输出,工作台不动),设其所记的数分别为
插补的过程中x轴和y轴的输出插补脉冲(此脉冲不输出,工作台不动),设其所记的数分别为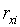 与
与![]() (i,j为插补脉冲序号)。当达到
(i,j为插补脉冲序号)。当达到 ![]() 时,停止插补运算,这时
时,停止插补运算,这时![]() 及
及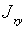 中所存的数就是刀具半径r在x轴和y轴上的分量
中所存的数就是刀具半径r在x轴和y轴上的分量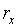 和
和![]() 。
。
有了 ![]() 、
、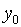 及
及 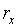 、
、![]() ,就可作加法运算
,就可作加法运算
![]() +
+ 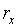 =
=![]()
即 (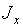 )+(
)+(![]() )
)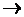
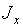
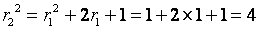
图2-46
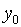 +
+![]() =
=![]()
即 (![]() )+(
)+(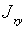 )
)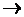
![]()
这样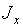 和
和![]() 中寄存的就是
中寄存的就是![]() 点的坐标值
点的坐标值![]() 及
及![]() 了。
了。
下面讨论![]() 的判别。
的判别。
首先求![]() 值。对于拨盘输入的r值,为了避免作平方运算,可以用递推法来求
值。对于拨盘输入的r值,为了避免作平方运算,可以用递推法来求![]() ,这就要多用
,这就要多用![]() 和
和![]() 两条寄存器,如图2-46所示。
两条寄存器,如图2-46所示。
计算的递推公式如下:
![]() =
= ![]() +1
+1
![]() =
= ![]()
用![]() 存放
存放 ![]() 值,
值,![]() 存放
存放![]() 值,并设运算开始时
值,并设运算开始时![]() =
=![]() =0,按图2-46逻辑线路逐次求和,结果如下:
=0,按图2-46逻辑线路逐次求和,结果如下:
第一次相加:![]() =
= ![]() +1=0+1=1
+1=0+1=1
![]()
第二次相加:![]()
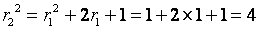
第三次相加:![]()
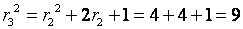
……
依次递推,直到 ![]() 中之值和刀具半径r相等为止。而
中之值和刀具半径r相等为止。而![]() 中的数值即为
中的数值即为![]() 。
。
对于 ![]() 是否成立亦可按下式用递推法来进行判别。
是否成立亦可按下式用递推法来进行判别。
![]() =
= ![]()
在作刀具偏移直线插补过程中,除了用![]() 和
和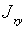 分别寄存
分别寄存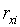 和
和![]() 外,还需有一条寄存器
外,还需有一条寄存器![]() 来寄存判别值
来寄存判别值![]() 。
。
每当![]() 记入一个脉冲时计算:
记入一个脉冲时计算:
![]() =
= ![]() +
+![]() +1
+1
每当![]() 记入一个脉冲时计算:
记入一个脉冲时计算:
![]() =
= ![]() +
+ ![]() +1
+1
初始时,令![]() =0;
=0;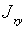 =0;
=0;![]() =-
=- ![]() 。在刀具半径偏移插补过程中,每发出一个插补脉冲,就进行一次
。在刀具半径偏移插补过程中,每发出一个插补脉冲,就进行一次![]() 运算,并且判别是否为零。当
运算,并且判别是否为零。当![]() =0时,就满足
=0时,就满足![]() 的条件,停止插补运算,这时存放在
的条件,停止插补运算,这时存放在![]() 和
和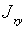 中的数据就是r在x轴和y轴上的分量
中的数据就是r在x轴和y轴上的分量 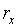 和
和 ![]() (
(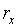 ,
,![]() 值即为刀具半径补偿值)。由于此原理在计算刀偏值时须使用刀具半径r的平方值,因而被称为
值即为刀具半径补偿值)。由于此原理在计算刀偏值时须使用刀具半径r的平方值,因而被称为![]() 法。
法。


