设一圆以坐标原点为圆心，则其方程为
（2－40）
考虑起点为
、终点为
的第Ⅰ象限顺圆弧
，如图2-33所示。
图2-33
对式（2-40）两边微分得
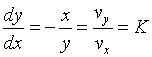
亦即有
对上式用矩形公式求积就得到
亦即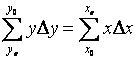 
令 
（即脉冲当量=1）
； 
经变量替换，上面的积分求和公式变为
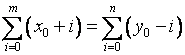（2－41）
上式的展开式为
+（+1）+（+2）+…=
+（-1）+（-2）+…
图2-34
公式（2-41）表示，若用进给脉冲的时间间隔来描述圆的动点变化规律，则圆函数的脉冲时间间隔在插补过程中是变化的，在某一时刻x轴与y轴进给脉冲时间间隔之比等于动点所在位置圆的半径矢量的x分量与y分量之比。公式（2-41）是公差分别为+1和-1的等差数列，圆就可根据这组等差数列来产生。根据式（2-41）可作出如图2-34所示的第Ⅰ象限顺圆弧进给脉冲分配序列。
同理，不难得出圆函数在不同象限顺、逆时针加工情况下的矩形求和公式。
第Ⅰ、Ⅲ象限顺圆，第Ⅱ、Ⅳ象限逆圆矩形求和公式为
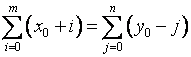（2-42）
第Ⅱ、Ⅳ象限顺圆，第Ⅰ、Ⅲ象限逆圆矩形求和公式为
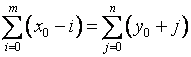（2-43）
为实现圆函数插补运算也须要引进判别函数
。所不同的是除偏差运算外，在
轴（或
轴）每发出一个进给脉冲后，还得对被积函数（或）作加1或减1修正。
