我们先用直线插补来说明。在数字积分法的介绍中已经知道,一个函数的定积分可以用矩形公式求和来近似计算。
如果已知一条直线的方程为
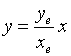 (2-37)
(2-37)
式中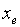 ,
,![]() 为直线的终点坐标。
为直线的终点坐标。
对上式求微分得 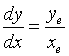
如果引入时间变量 ![]() ,分别对被积函数
,分别对被积函数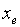 和
和![]() 进行积分就得到数字积分法的直线插补。我们现在不这样做,而是设法用比较判别的方法来建立两个积分的联系。先将上式改写为
进行积分就得到数字积分法的直线插补。我们现在不这样做,而是设法用比较判别的方法来建立两个积分的联系。先将上式改写为
![]()
用矩形公式来求积就得到
![]()
或 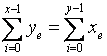 (2-38)
(2-38)

图2-32 脉冲分配序列
此式表明,![]() 方向每发一个进给脉冲,相当于积分值增加一个量
方向每发一个进给脉冲,相当于积分值增加一个量![]() ;
;![]() 方向每发一个进给脉冲,积分值增加一个量
方向每发一个进给脉冲,积分值增加一个量 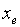 ,为了得到直线,必须使两个积分相等。
,为了得到直线,必须使两个积分相等。
根据式(2-38),我们在时间轴上分别作出x轴和y轴的脉冲序列,如图2-32所示。把时间间隔作为积分增量,轴上每隔一段时间![]() 发出一个脉冲,就得到一个时间间隔
发出一个脉冲,就得到一个时间间隔![]() ;y轴上每隔一段时间
;y轴上每隔一段时间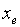 发出一个脉冲,就得到一个时间间隔
发出一个脉冲,就得到一个时间间隔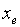 。在
。在![]() 轴发出
轴发出![]() 个脉冲后,其总时间间隔为式(2-38)的左边,即
个脉冲后,其总时间间隔为式(2-38)的左边,即
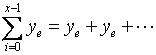
同样,如果![]() 轴上发出了
轴上发出了![]() 个脉冲,其总的时间间隔为积分式(2-38)的右边,即
个脉冲,其总的时间间隔为积分式(2-38)的右边,即
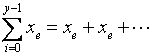
由公式(2-38)可知,要实现直线插补,必须始终保持上述两个积分式相等。为此,与逐点比较法相似,我们引入一个判别函数,所不同的是,这个判别函数定义为![]() 轴脉冲总时间间隔与
轴脉冲总时间间隔与![]() 轴脉冲总时间间隔之差。用
轴脉冲总时间间隔之差。用![]() 表示为
表示为 ![]()
 (2-39)
(2-39)
用一个脉冲源控制运算速度,每发一个脉冲,计算一次![]() 的值,根据
的值,根据![]() 的正负决定下次脉冲应如何进给。即当
的正负决定下次脉冲应如何进给。即当![]() >0时,说明
>0时,说明![]() 轴输出脉冲时间超前(即多发出
轴输出脉冲时间超前(即多发出![]() ),这时应控制
),这时应控制![]() 轴进行
轴进行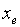 的累加;若
的累加;若![]() <0,则说明轴输出脉冲时间超前(即多发了
<0,则说明轴输出脉冲时间超前(即多发了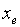 ),这时应控制
),这时应控制![]() 轴进行
轴进行![]() 的累加;依次进行下去即可实现直线插补。这里,我们通过将两个积分式相比较的办法来实现插补的,所以称为比较积分法。
的累加;依次进行下去即可实现直线插补。这里,我们通过将两个积分式相比较的办法来实现插补的,所以称为比较积分法。


