
图2-36直线插补轨迹
(1) 卦限的划分。直接函数法将直角坐标的每个象限都用45°斜线分成2个区域,如图2-36所示。图2-36卦限的划分4个象限共分为8个区域,称为8个卦限,用0~7表示。对某一卦限内的直线进行插补时,只有![]() 和
和![]() ,
,![]() 两种可能的进给方向。对于第Ⅰ象限的右下区域即“0”卦限来讲,直线插补时或是
两种可能的进给方向。对于第Ⅰ象限的右下区域即“0”卦限来讲,直线插补时或是![]() 方向走一步,或是
方向走一步,或是![]() 与
与![]() 方向同时走一步。对于“1”卦限的直线插补,或是
方向同时走一步。对于“1”卦限的直线插补,或是![]() 方向走一步,或是
方向走一步,或是![]() 与
与![]() 方向同时走一步。引入
方向同时走一步。引入![]() 和
和![]() 坐标系的目的是将8个卦限的进给都统一用“0”卦限内的u和v坐标来计算,以简化插补程序,缩短运算时间。对8个卦限中的直线,这种坐标变换关系如表2-9所示。
坐标系的目的是将8个卦限的进给都统一用“0”卦限内的u和v坐标来计算,以简化插补程序,缩短运算时间。对8个卦限中的直线,这种坐标变换关系如表2-9所示。
表2-9 直线插补的坐标变换
| 卦 限 | u | v |
| 0 | +x | +x, +y |
| 1 | +y | +x, +y |
| 2 | +y | -x, +y |
| 3 | -x | -x, +y |
| 4 | -x | -x, -y |
| 5 | -y | -x, -y |
| 6 | -y | +x, -y |
| 7 | +x | +x, -y |
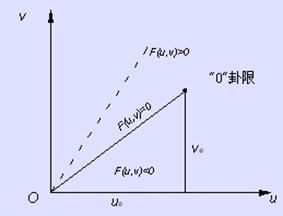
图2-37 “0”卦限的直线
(2) 误差函数与进给方向。图2-37中所示“0”卦限的直线终点为![]() 和
和![]() ,直线方程为
,直线方程为
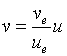
引入误差函数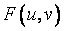 =
=![]() -
-![]() ,显然,对于直线上的所有点均满足下式:
,显然,对于直线上的所有点均满足下式:
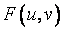 =
=![]() -
-![]() =0
=0
对直线上方的点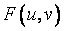
![]() 0
0
对直线下方的点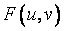
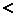 0
0
当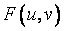
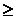 0时,往+
0时,往+![]() 方向进给一步,误差函数的变化为
方向进给一步,误差函数的变化为
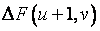 =
= ![]() -
-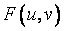
= ![]() -
-![]() -
- ![]()
=-![]() (2-44)
(2-44)
当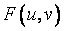
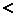 0时,往+
0时,往+![]() 和+
和+![]() 方向同时进给一步,误差函数的变化为
方向同时进给一步,误差函数的变化为
![]() =
= 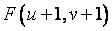 -
- 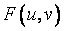
= ![]() -
-![]() -
- ![]()
= ![]() (2-45)
(2-45)
在插补过程中,引入进给循环变量![]() 可得
可得
![]() (
(![]() +1)=
+1)=![]() (
( ![]() )+
)+ ![]()
因插补是从坐标原点开始的,故![]() (0)=0。在
(0)=0。在![]() 方向进行终点判别,当
方向进行终点判别,当![]() =
= ![]() 时,直线到达终点,插补工作完成。
时,直线到达终点,插补工作完成。
图2-38是对![]() =30,
=30,![]() =4的“0”卦限直线进行插补的例子。为了直观,图中的脉冲当量取得很大。从图中可以看出,进给方向的变化不是90°而是45°。
=4的“0”卦限直线进行插补的例子。为了直观,图中的脉冲当量取得很大。从图中可以看出,进给方向的变化不是90°而是45°。
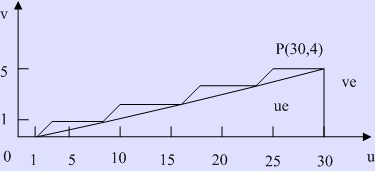
图2-38 “0”卦限的直线插补轨迹
为了减小插补误差,实际的DFB法还可以进一步对两个可能的进给方向作试算与比较,并选择一个误差最小的方向进给。
若往![]() 方向进给一步,误差函数将为
方向进给一步,误差函数将为
![]()
若![]() 和
和![]() 方向同时都进给一步,误差函数将为
方向同时都进给一步,误差函数将为
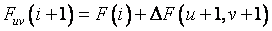
将式(2-44)和式(2-45)分别代入上两式中,可得到两个试算结果,将它们的绝对值进行比较,以决定应向哪个方向进给。
当|![]() |
|![]() |
|![]() |时,
|时,![]() +1次进给应为
+1次进给应为![]() 方向;
方向;
当|![]() |
|![]() |
|![]() |时,
|时,![]() +1次进给应为
+1次进给应为![]() 和
和![]() 方向(即各进给一步)。
方向(即各进给一步)。


