图2-39是第Ⅰ象限的逆时针方向圆弧，圆心在xoy坐标系的原点。参考圆的方程，引进误差函数F(x,y)=x2+y2-r2用来选择适当的进给方向。
对于圆弧上的点
F(x,y)=x2+y2-r2=0 （2-46）
对于圆外的点
F(x,y)>0
对于圆内的点
F(x,y)<0
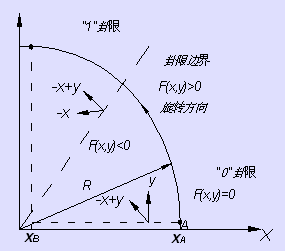
图2-39 第Ⅰ象限圆弧
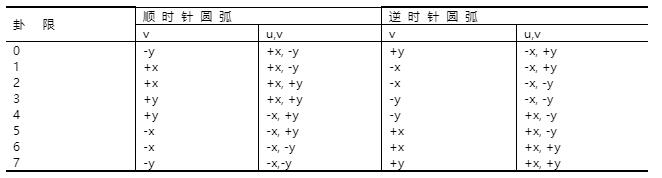
图2-40 圆弧插补各卦限的进给方向
为了使进给方向每次最多改变45°，仍旧划分0～7共8个卦限，将各卦限内的圆弧插补，都统一用“0”卦限的公式进行计算。每个卦限中又都有顺时针圆弧和逆时针圆弧两种情况，8个卦限中顺圆与逆圆的进给方向标在图2-40中，均用 v和 u， v代表。它们在xoy 坐标系中的实际进给方向可根据卦限及圆弧走向用表2-10进行变换。显然，当每次插补运算时，除判断是否到达终点外，还要判断是否到达卦限的边界。如图2-39中第Ⅰ象限的逆圆在“0”卦限限时，它是沿+ y向或- x和+ y向进给的，到达“1”卦限的边界后，应改为沿- x向或- x和+ y向进给。
表2-10 直线插补时进给方向的坐标变换
将公式（2-46）转换为u和v坐标，并在“0”卦限中推导误差函数的变化。对逆时针圆弧，当F>0时，应走+V和-U；当F<0时，应走+V。当往+V走一步时
=
=2V+1 （2-47）
而往-U与+V向同时走一步时
=
= 
=-2U+2V+2 （2-48）
对顺时针圆弧，则或者走-v（F>0时），或者走+u和-v（F<0时）。当往-v向走一步时，可求出
=-2V+1 （2-49）
往+u与-v向同时走一步时，可求出
=2U-2V+2 （2-50）
引入循环变量i可得
F（i+1）= F（i）+ΔF（i+1）
当i=0时，为圆弧上的起始点（如图2-39中的A点）。此时 F（0）=0。
当 F（i）>0时，轨迹到达圆外。此时，对于“0”或偶数卦限的逆时针圆弧及奇数卦限的顺时针圆弧，i+1次进给应为u和v方向。对于奇数卦限逆时针圆弧及“0”或偶数卦限顺时针圆弧，i+1次进给应为
方向。
当F（i）<0时，轨迹则到达圆上或进入圆内。此时，对“0”或偶数卦限的逆时针圆弧及奇数卦限的顺时针圆弧，i+1次进给应为方向。对于奇数卦限的逆时针圆弧及“0”或偶数卦限的顺时针圆弧，i+1次进给应为u和v方向。
以上各种情况下的实际进给方向，可参照表2-10得到。误差函数计算统一使用“0”卦限中推导的公式（2-47）、（2-48）（逆时针圆弧）或（2-49）、（2-50）（顺时针圆弧）。为此，要统一变换为u和v坐标，且u和v坐标的走向与实际进给方向的关系要与图2-40中“0”卦限情况一样。
除根据误差函数、卦限及圆弧走向判断本次应进给的方向外，插补运算还包括下列步骤：
（1） 计算
F（i+1）；
（2） 修正并得到新的坐标值u（i+1）和v（i+1）；
（3） 存入应进给方向的符号；
（4） 计算误差函数F（i+1）；
（5） 检查进给后是否到达卦限的边界；
（6） 检查进给后是否到达预定圆弧的终点。
除了直线插补与圆弧插补外，DFB法还可以推广到用方程
描述的一般二次曲线。但由于在计算误差函数时，要与各系数作乘法运算，将使插补运算的速度显著变慢。在这种情况下，只好损失一些进给速度，而对于像抛物线这种二次曲线的特例，用直接函数法进行插补运算的速度则与圆弧插补时相当。此外，DFB法也可以推广到极坐标。这时，阿基米德螺旋线的插补可以归并为直线插补。
