如图1所示,滚刀剃后齿顶修缘量为δ,修缘高度为ft。在一般情况下,只要能满足加工条件,应使剃后齿轮的修缘角αd和修缘高度ft尽可能大(但当模数mn≤3时,ft最好不大于0.5)。可见,修缘尺寸的确定是一个双参数优化问题。笔者在编制计算修缘尺寸的计算机程序时,采取了以下优化步骤:
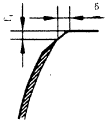
图1 齿轮齿顶修缘
(1)初始赋值时,对于剃后齿顶修缘量δ和修缘高度ft,如图纸上有明确要求,则按要求值输入;如图纸上未作要求,则可根据模数mn和齿数z合理赋以较大的初始值,如mn=2,z=30时,可令δ=0.3,ft=0.45。对于修缘角αd,可先令αd=30°。
(2)如图2所示,由ft和αd求出滚刀上修缘起始点至齿顶的高度hd,并判断hd≥1.95mn是否成立,如不成立,则按步长0.01递减ft后重新运算。如此循环运行,直至ft不小于0.3时为止。
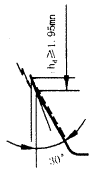
图2 滚刀修缘起始点
(3)ft确定后,按步长1″递增αd,直至计算出的齿轮递后齿顶修缘量δ满足要求为止,此时的αd即为最大修缘角,如图3所示。
(4)根据hd和αd求出滚刀齿根槽间宽Wi(见图3)。
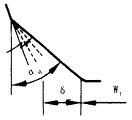
图3 求最大修缘角
(5)判断求得的齿根槽间宽Wi能否满足Wi≥W(W为能修出齿根圆弧R2的最小槽宽),如Wi过小,可按以下方法解决:①若ft>0.35,则可继续按步长0.01递减ft,而αd保持不变,即同时减小ft和δ以增大Wi,如图4所示。②若ft≤0.35,则只减小αd以增大Wi,如图5所示。但应注意,此时W因αd的改变也在同时改变。显然,αd减小时,δ也相应减小,因此,当αd递减至30°而Wi仍不能满足Wi≥W的要求时,为避免δ过小,则应将R2适当减小。
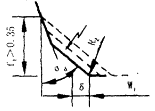
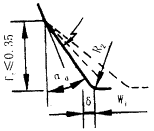
图4 修缘角αd不变 图5 减小修缘角αd
(6)最后确定αd,并计算出δ。
在上述优化过程中,均限定了循环下限,实际上,只要齿轮的参数、尺寸设计合理,一般不会出现达到循环下限仍无法满足优化条件的情况,如果出现这种情况,则说明该齿轮无需进行修缘。