生产实际中,影响加工误差的因素往往是错综复杂的,有时很难用单因素来分析其因果关系,而要用数理统计方法进行综合分析来找出解决问题的途径。
一、加工误差的性质
各种单因素的加工误差,按其统计规律的不同,可分为系统性误差和随机性误差两大类。系统性误差又分为常值系统误差和变值系统误差两种。
(一)系统性误差
l .常值系统误差
顺次加工一批工件后,其大小和方向保持不变的误差,称为常值系统误差。例如加工原理误差和机床、夹具、刀具的制造误差等,都是常值系统误差。此外,机床、夹具和量具的磨损速度较慢,在一定时间内也可看作是常值系统误差。
2 .变值系统误差
顺次加工一批工件中,其大小和方向按一定的规律变化的误差,称为变值系统误差。例如机床、夹具和刀具等在热平衡前的热变形误差和刀具的磨损等,都是变值系统误差。
(二) 随机性误差
顺次加工一批工件,出现大小和方向不同且无规律变化的加工误差,称为随机性误差。例如毛坯误差 (余量大小不一、硬度不均匀等 )的复映、定位误差 (基准面精度不一、间隙影响 )、夹紧误差 (夹紧力大小不一 )、多次调整的误差、残余应力引起的变形误差等,都是随机性误差。
随机性误差从表面看来似乎没有什么规律,但是应用数理统计的方法可以找出一批工件加工误差的总体规律,然后在工艺上采取措施来加以控制。
二、加工误差的统计分析法 ( 分布图分析法 )
统计分析是以生产现场观察和对工件进行实际检验的数据资料为基础,用数理统计的方法分析处理这些数据资料,从而揭示各种因素对加工误差的综合影响,获得解决问题的途径的一种分析方法,主要有分布图分析法和点图分析法等。本节主要介绍分布图法。其他方法请参考有关资料。
1 .实际分布图 ——直方图
在加工过程中,对某工序的加工尺寸采用抽取有限样本数据进行分析处理,用直方图的形式表示出来,以便于分析加工质量及其稳定程度的方法,称为直方图分析法。
在抽取的有限样本数据中,加工尺寸的变化称为尺寸分散;出现在同一尺寸间隔的零件数目称为频数;频数与该批样本总数之比称为频率;频率与组距 (尺寸间隔 )之比称为频率密度。
以工件的尺寸 (很小的一段尺寸间隔 )为横坐标,以频数或频率为纵坐标表示该工序加工尺寸的实际分布图称直方图,如图 4-32所示。
直方图上矩形的面积=频率密度×组距 (尺寸间隔 )=频率
由于所有各组频率之和等于 100%,故直方图上全部矩形面积之和等于 l。
下面通过实例来说明直方图的作法:
例如磨削一批轴径为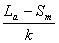 mm的工件,实测后的尺寸如表 4-3所示。
mm的工件,实测后的尺寸如表 4-3所示。
表 4-3 轴径尺寸实测值 (μ m)
| 44 | 20 | 46 | 32 | 20 | 40 | 52 | 33 | 40 | 25 | 43 | 38 | 40 | 41 | 30 | 36 | 49 | 51 | 38 | 34 |
| 22 | 46 | 38 | 30 | 42 | 38 | 27 | 49 | 45 | 45 | 38 | 32 | 45 | 48 | 28 | 36 | 52 | 32 | 42 | 38 |
| 40 | 42 | 38 | 52 | 38 | 36 | 37 | 43 | 28 | 45 | 36 | 50 | 46 | 38 | 30 | 40 | 44 | 34 | 42 | 47 |
| 22 | 28 | 34 | 30 | 36 | 32 | 35 | 22 | 40 | 35 | 36 | 42 | 46 | 42 | 50 | 40 | 36 | 20 | 16 Sm | 53 |
| 32 | 46 | 20 | 28 | 46 | 28 | 54 La | 18 | 32 | 33 | 26 | 46 | 47 | 36 | 38 | 30 | 49 | 18 | 38 | 38 |
注:表中数据为实测尺寸与基本尺寸之差。
作直方图的步骤如下:
(1)收集数据。一般取 100件左右,找出最大值 La= 54μ m,最小值 Sm= 16μ m(见表 4-1)。
(2)把 100个样本数据分成若干组,分组数可用表 4-4确定。
表 4-4 样本与组数的选择
| 数据的数量 | 分组数 |
| 50 ~ 100 | 6 ~ 10 |
| 100 ~ 250 | 7 ~ 12 |
| 250 以上 | 10 ~ 20 |
本例取组数 k= 8。经验证明,组数太少会掩盖组内数据的变动情况,组数太多会使各组的高度参差不齐,从而看不出变化规律。通常确定的组数要使每组平均至少摊到 4~ 5个数据。
(3)计算组距 h,即组与组间的间隔
h =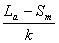 =
=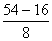 =4.75 μ m ≈ 5μ m
=4.75 μ m ≈ 5μ m
(4)计算第一组的上、下界限值
Sm±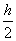
第一组的上界限值为 S m+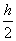 =( 16+
=( 16+ 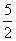 )μ m = 18.5μ m;
)μ m = 18.5μ m;
下界限值为Sm-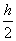 =(16-
=(16-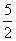 )μm = 13.5μm。
)μm = 13.5μm。
(5)计算其余各组的上、下界限值。 第一组的上界限值就是第二组的下界限值。第二组的下界限值加上组距就是第二组的上界限值,其余类推。
(6)计算各组的中心值 X i。中心值是每组中间的数值。
Xi = (某组上限值 +某组下限值) / 2
第一组中心值 Xi= Xi=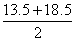 μm=16μm
μm=16μm
(7)记录各组的数据,整理成频数分布表,如表 4-5所示。
(8)统计各组的尺寸频数、频率和频率密度,并填入表中。
(9)按表列数据以频率密度为纵坐标;组距(尺寸间隔)为横坐标就可以画出直方图,如图 4-32所示
| 组数n | 组界/μm | 中心值χi | 频数统计 | 频数mi | 频率/% | 频率密度/(μm-1)(%) |
| 1 | 13.5~18.5 | 16 | ||| | 3 | 3 | 0.6 |
| 2 | 18.5~23.5 | 21 | ||||||| | 7 | 7 | 1.4 |
| 3 | 23.5~28.5 | 26 | |||||||| | 8 | 8 | 1.6 |
| 4 | 28.5~33.5 | 31 | ||||||||||||| | 13 | 13 | 2.6 |
| 5 | 33.5~38.5 | 36 | |||||||||||||||||||||||||| | 26 | 26 | 5.2 |
| 6 | 38.5~43.5 | 41 | ||||||||||||||||||| | 16 | 16 | 3.2 |
| 7 | 43.5~48.5 | 46 | ||||||||||||||||||| | 16 | 16 | 3.2 |
| 8 | 48.5~53.5 | 51 | |||||||||||| | 10 | 10 | 2 |
| 9 | 53.5~58.5 | 56 | | | 1 | 1 | 0.2 |
表 4-5 频数分布表
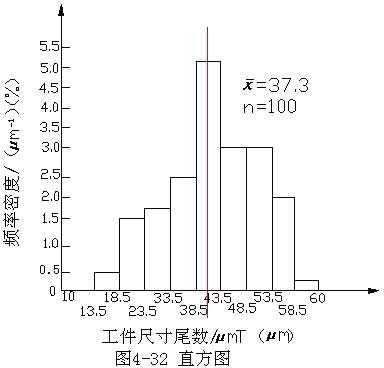
由图 4-32可知,该批工件的尺寸分散范围大部分居中,偏大、偏小者较少。
尺寸分散范围 = 最大直径 – 最小直径 = 60.054 – 60.016 = 0.038mm
尺寸分散范围中心 :
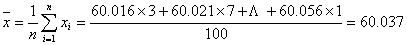 mm
mm
直径的公差带中心 = 60+ 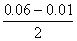 = 60.025 mm
= 60.025 mm
标准差为 : 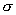 =
=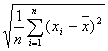 =
=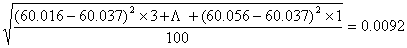 = mm
= mm
从图中可看出 ,这批工件的分散范围为 0.038,比公差带还小,但尺寸分散范围中心与公差带中心不重合,若设法将分散范围中心调整到与公差带重合,即只要把机床的径向进给量增大 0.012 mm,就能消除常值系统误差。