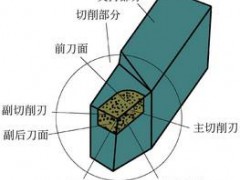
对于2D轮廓加工,除了调整刀具进给率,在调节切削角度和切削力上,刀具路径修正方法已经成为一种颇具吸引力的方法,并且很可靠。要使得整个加工过程中保持进给率的恒定,即使在没有高性能的机床伺服器调节进给切削角度和切削力,也可以通过刀具路径修正的方法来实现。在2D加工中,对工字形简单二维轮廓直接采用通用等距算法外(内)偏置一个刀具半径得到凸台(凹槽)加工刀轨,加工出凸台和凹槽的轮廓形状。但是,由于这种加工方法所生成的刀具路径已经不是所期待的工件轮廓线,不适用于型腔内壁的由里向外的加工。Stori和Wright首先提出前向刀具路径修正方法。本课题提出对这个算法的修正算法,以便它可以应用于任意几何的刀路,并在试验中验证此算法。
Stori和Wright算法
1 传统前向刀具路径修正算法
为了保持一个恒定的切削进给,对凸包几何体的稳定切削过程,Stori和Wright提出了一个著名的方法来修正刀具路径。这个方法在2D轮廓加工中产生恒定的修正刀路。
给定一条初始的平面曲线,这条曲线表示了即将要加工的曲面轮廓。由一系列点P(i)∈R2(i=1,…,Np)表示。这个算法的主要目的是产生1个新的偏置加工曲面轮廓和一系列刀具中心位置,以便可以在整个加工时间内保持一个恒定的进给。图1 是Stori和Wright提出的刀具路径修正算法的简化示意图。假定在给定点上已知下列变量:P(i),P(i+1)——当前刀具和工件曲面的相交点以及紧接着的下个相交点;Q(i)∈R2(i=1,…,NQ)——刀具和最新加工过的工件曲面的相交点。
给定刀具半径r和所需要的切削角度可以调节α*en 得到。新的偏置曲面点Q(i+1)∈R2(i=1,…,NQ)和修正过的刀具中心位置O (i+1)∈R2(i=1,…,NO),具体算法如下。
(1)通过下列方程计算新的偏置曲面点Q(i+1)。
Q(i+1)=Q(i)+λT(i) ①
以便
Q(i) + λT (i) − P (i + 1) = l ②
其中,l是腰长为r且两腰夹角为切削角度α *e n 的底长, 即l =2r2 ??1 − cos α∗en,并且T(i)∈R2,是新偏置曲面的单位切矢量,如图1所示。
(2)通过以下方程计算在新偏置曲面的单位切矢量。
T (i + 1) =P (i + 1) − Q(i + 1) P (i + 1) − Q(i + 1) cos φ − sin φsin φ cos φ ③
其中,φ是单位切矢量的倾斜角;T(i)是矢量 P(i+1)-Q(i+1)
(3)通过以下方程计算刀具中心位置O(i+1)。
O(i + 1) = Q(i + 1) + r ·T (i + 1)cosπ2 − sin π2sin π2 cos π ④
(4)设i=i+1,并且重复步骤①~④,直到刀具走完整条加工路径。值得注意的是,由上面算法生成的刀具中心位置仅可以应用于由P(i)定义成的凸包几何曲面。当应用于非凸几何曲面则是不可行的。在实际中,特别是模具加工中,经常有复杂的集合体和几乎不能满足的凸包条件,所以此算法必须通过改进才可以应用于实际加工中。
2 前向刀路修正算法
本课题组根据Stori和Wright所提出的2D轮廓加工算法,提出了一种新的方法来生成一种恒定进给率的刀具路径,以便这种算法可以应用于包括凸状和凹状的任意类型的几何刀路。基本算法如图2所示。不同于Stori和Wright给出的算法,提出的前向刀路修正算法不能在数学上保证收敛于一个优化的结果。然而,该算法最大的一个优点是它可以应用到任意2D几何轮廓,不像Stori和Wright的算法,仅限于凸几何。
对于恒定切削进给的后向刀具路径修正算法
目前,本课题组又提出了一种新的方法来生成一种恒定进给率的刀具路径,以便这种算法可以应用于包括凸状和凹状的任意类型的几何刀路。
用1条初始的平面曲线来表示需要加工零件的几何轮廓,并且提供1条原始的轮廓偏置曲线,这条曲线就是需要的精加工刀具路径,可以从NC代码中提取。这个算法的主要目的就是计算相对精加工路径的前1条完整的刀具路径,称其为半精加工路径。对半精加工路径进行修正,使得刀具在最后的精加工路径中可以以恒定的速率进行加工,并且取得恒定的切削量。此研究关注的是由直柄平头端铣刀进行的2D轮廓加工,并且只考虑刀具和工件之间的干涉。
这里所提到的“刀具路径修正”可以做如下理解,就是对于给定的最后的精加工路径,通过修正使得刀具以所需要的恒定的切削角度来进行加工,并且本课题所提出的算法目的是对半精加工刀路进行修正,也就是修正刀具圆周和半精加工曲面Pk (i)的交点位置,从而得到一个新的位置P*k(i)。用这种方法使得切削进给角度从α*e(n i)调节到所需要的α*e(n i)。半精加工路径Pk(i)的修正可以通过对Ok-1(i)的修正做到。新的半精加工路径O*k-1(i)可以通过简单的偏置P*k(i)给出。O*k-1(i)的详细算法可以按照如下步骤进行计算。
(1)假设在精加工中,刀具中心的轨迹为Q(i)∈R2(i=1,…,Nk)。这条轨迹也就是被加工零件的轮廓按照刀具半径所偏置的1 条曲线,如图3 所示。进给角度αen(i)∈R2(i=1,…,NQ)可以由刀具中心位置Ok(i),刀具与新加工的曲面接触点Qk(i)∈R2(i=1,…,Nk),刀具与半精加工曲面上的点Pk(i)∈R2(i=1,…,Nk),这3个点所组成。半精加工曲面Pk(i)的生成先于精加工,其加工路径为Qk-1(i)∈R2(i=1,…,Nk-1)。
(2)对于在精加工中给定的刀具中心位置Qk-1(i)∈R2(i=1,…,Nk-1),可以将Qk(i)向工件加工区域偏置1个刀具半径r,从而计算出刀具圆周和新加工的零件曲面的交点。这个操作可以表示为:
Qk(i)= offset(Qk(i),+ r)(i=1,…,Nk) ⑤
其中,函数offset(Q(i),x)表示了通过平行偏执轨迹Q(i)1个x的距离所生成的轨迹。#p#副标题#e#
(3)计算出所需要的相交点P*k(i),即半精加工面和刀具周围的相交点。此计算是为了使得进给角度αen(i)满足需要的精加工角度α*en(i),即寻找P*k(i),使得∠P*k(i)·Ok(i)·Ok(i)=α*en(i),并且||P*k(i)-Ok(i)|| =r(i=1,…,Nk)。其中,“∠”表示了由点构成的角度。P*k(i)定义了修正过的半精加工路径,如图3所示。
(4)使i=i+1,并且重复步骤③和④,直到i=Nk。
(5)通过偏置半径加工区面轨迹P*k(i)1个刀具半径r,计算出半精加工的修正刀具中心轨迹:O*k-1(i)∈ R2(i=1,…,Nk-1)。这样O*k-1(i)= offset(P*k(i),- r)( i=1,…,Nk-1)。
(6)对于给定的刀具和工件,当计算出了所需要的进给角度α*en(i)后,就可以使得刀具在精加工阶段始终维持一个恒定的切削力。
反向刀具路径修正的应用实例
1 仿真试验
通过具体的试验来验证后向刀具路径修正算法的有效性。本试验将在切削力、集合误差和加工时间方面与传统的方法进行对比。
在本试验中,所需要的切削角度α*en 可以通过以下步骤得到。假定给定刀具半径为r,径向切削深度为s 的路径,那么在线性切削阶段的切削角度αen 可以计算出来;然后在本算法中应用αen(i)来计算所需要的进给切削角度α*en。其实也就是说,应用此算法是为了在整个加工阶段的切削角度不能偏离在线性加工阶段的水平。
如图4所示,采用一个简单的弯角几何作为实例。其中,s是径向切削深度,αen为进给切削角度,r为刀具半径。图5中显示了本算法计算所得出的修正半精加工路径,传统的半精加工路径以及精加工路径。在精加工阶段,对传统半精加工和采用本算法进行修正的半精加工的切削角度进行了对比。从图6中可以明显看出,传统方法的切削角度从11.5°猛然跳至19°,这样就会造成加工的不稳定,从而使加工面质量不高;而本算法却可以使得刀具在整个精加工阶段维持一个比较好的进给角度变化水平。曲线中1个小的不连续的变化是由于线性和圆弧的连接点,这是由于在仿真中的计算误差造成的。
2 具体试验
在具体加工上来验证本算法的有效性。本试验使用1台高速三坐标加工中心,型号是proLIGHT 1000Machining Center,加工件的轮廓如图4所示。用于本试验的加工条件如表1所示。为了比较切削性能,采用了3种方法。
(1)加工策略1。
本加工方法采用传统的轮廓偏置加工方法,并且应用于半精加工和精加工中,在加工过程中保持进给率的恒定。
(2)加工策略2。
是应用于半精加工的恒定进给路径的修正方法,也就是后向刀具路径修正方法,而精加工路径和策略1 使用相同的路径,并且加工过程中始终维持恒定进给率。