1 前言
自由曲面在模具中应用非常广泛,如汽车车身模具、塑料模、叶片锻模、铸模等,大都包含自由曲面(以下简称曲面)。曲面的加工通常由球面刀和非球面刀(如平头立铣刀、锥状刀、鼓形刀等)完成,由于平头立铣刀(以下简称立铣刀)的切削效率、加工质量、使用寿命等都优于球面刀[1],应优先选择。近几年来,国内外有关曲面立铣刀五轴数控加工轨迹的算法的研究较多[4~6],这些算法用微分几何的方法对步长和行距进行预测,公式简单,计算量小,但它们没有考虑相邻刀具接触点间曲率的变化,对于加工曲率变化小的曲面比较有效,不适合曲率变化大的曲面。本文提出一种在参数坐标系下自适应步长和行距的计算方法。该算法在满足加工精度和粗糙度的前提下,又能有效地提高加工效率,适合曲率变化大的曲面的加工。
2 刀具的有效半径
五轴立铣加工曲面时,由于立铣刀的切削刃在立铣刀的周边上,所以立铣刀的轴线与曲面的法线之间应当偏置一个刀具半径,方能有效地切削曲面。考虑到刀具与曲面干涉等因素,立铣刀在偏置的同时,其轴线在被加工点的法平面内还应与法线夹一角度φ(图1),n为被切削曲面单位法向矢量,Tax为刀具单位轴向矢量,R为刀具半径,那么,刀具的有效切削半径定义为:Re=Rsinφ。在图1所示的状态下,其端面在被加工点的密切面上的投影为长半轴R、短半轴为Re的椭圆。若坐标原点在刀具端面的圆心上,以长、短半轴为坐标轴,立铣刀的端面的方程为:
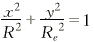 (1)
(1)

图1 刀具有效
为此,立铣刀切削曲面可以看作一把椭圆成形刀在加工曲面。
3 自适应步长的计算
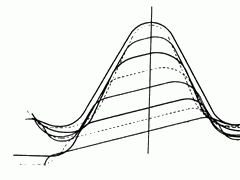
在五坐标数控加工过程中,由于曲面各处的法向矢量是变化的,必然会引起刀具轴向矢量的变化,即刀轴的摆动会使刀具与曲面的接触点轨迹不是一条直线,而是曲线。所以,五坐标立铣加工误差δ包括直线逼近误差δt和刀轴摆动误差δn(图2)。本算法选择曲面某一参数方向(如u向)作为步长进行误差控制(图3),点r(wi,0)、r(wi,1)为曲线r(wi,0)r(wi,1)上两点,连接点r(wi,0)、r(wi,1)成一弦,点r(wi,u)为曲线到弦r(wi,0)r(wi,1)的最大距离点,计算该点处的直线逼近误差和刀轴摆动误差,比较加工误差δ与允差ε的大小,若δ>ε,连接新的端点r(wi,u)、r(wi,0)形成新弦r(wi,0)r(wi,u),将新的参数曲线的区间[0,u]转换到[0,1]区间,再次计算加工误差δ,如此下去,直到δ<ε为止。记下此点Δu值,作为加工步长,再以r(u)为新起点,重复计算,即可算出每一点的步长。
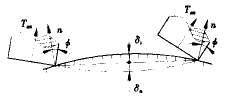
图2 步长误差的控制
3.1 直线逼近误差的计算
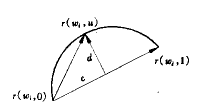
图3 直线逼近误差的计算
如图3所示,曲线r(wi,0)r(wi,1)的加工实际是通过插补多段内接弦来逼近它。考虑到加工效率,希望弦长尽量大,弦的段数尽量少,即在满足精度的情况下取最大的弦长来逼近,通常的办法是从曲线的一端开始采用迭代搜索法求取弦的另一端点。连接点r(wi,0)、r(wi,1)成一弦,若弦r(wi,0)r(wi,1)用矢量c表示,d表示曲线上的点到弦r(wi,0)r(wi,1)的最大距离,即δt=|d|。
那么存在:d=r(wi,u)-r(wi,0)-λc (2)
式中:λ——系数,λ∈[0,1]。
由于c与d垂直,可得到:
cd=0 (3)
联立式(2)、(3)解得:
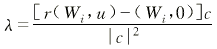 (4)
(4)
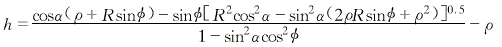 (5)
(5)
上式可以写成:
d=P[r(wi,u)-r(wi,0)] (6)
其中,1,称为投影矩阵,I为单位矩阵。
由于在弦向偏差最大处,曲线切矢垂直于矢量d,即r′((wi,u)d=0 (7)
故r′((wi,u)P[r(wi,u)-r(wi,0)]=0 (8)
上式中除两端点为根外,还有多个根,由于在弦向偏差最大处,存在:
r″(wi,u)d<0 (9)
所以把式(8)和u∈(0,1)用于每一个根处,式(7)中满足式(8)和u∈(0,1)的根即为最大偏差处相应的u值,因此,可求出δt。
上述算法过程中,首先必须检查曲线段内有无拐点,并计算出该点的位置。若曲线段有拐点,则以此拐点将曲线一分为二,将两段参数曲线的区间[u1,u2]转换到[0,1]区间,分别对两段曲线采用二分法进行迭代。
3.2 刀轴摆动误差的计算
刀轴摆动误差是加工过程中,由于刀具轴向矢量摆动引起的非线性误差(见图2)。可以证明[6]:
|δn|≤Re(kf.ΔSu) (10)
式中:kf——直线逼近段内曲面沿进给方向在最大直线逼近误差点处的法曲率;
ΔSu——逼近段弧长。
ΔSu=∫u2u1|r′(Wi,u)|du (11)
当kf<0时,加工表面沿走刀方向为凸曲线,刀具接触点的轨迹为凹曲线,因此,加工误差为直线逼近误差和刀轴摆动误差绝对值之和,即:δ=|δn|+|δt|。
当kf<0时,加工表面沿走刀方向为凹曲线,刀具接触点的轨迹亦为凹曲线,且刀轴摆动误差|δn|总是小于直线逼近误差|δt|,因此,可视直线逼近误差|δt|为加工误差δ,即:δ=|δt|。
4 自适应行距的计算
虽然曲面的形状各异,但是刀具在加工这些曲面时,都是按照一定的曲线走刀加工出整张曲面的。对于刀具接触点而言,根据其所在曲线在该点处的曲率大小可以分为三类:凸点、凹点、拐点,在这里将直线上的点也归为拐点类。凸点、凹点、拐点可以根据其曲率kf的大小加以判别:
当kf>0时,为凸点;
当kf<0时,为凹点;
当kf=0时,为拐点。
与凸点、凹点、拐点相对应,这些点所在的曲线可以分为凸曲线、凹曲线、直线。当刀具的接触点是凸点、凹点或拐点时,在密切面内,这三类点邻域的曲线可以分别看成是凸圆弧、凹圆弧和直线。因此,在计算自由曲面的行距时,可以直接在圆弧和直线上加以计算。
图4a为立铣刀加工凸曲面时的情形,ρ为刀具接触点处的曲率半径,ΔSw为行距,椭圆代表立铣刀,刀具接触点分别为B、C两点,即点r(w1,ui)、r(w2,ui),设坐标原点在立铣刀的中心上,那么,A点的坐标为:
x=(ρ+h)sinα
y=(ρ+h)cosα-(ρ+Rsin)
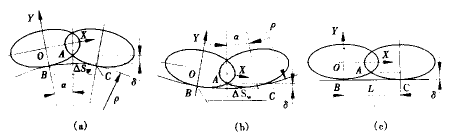
图4
(a)凸曲线 (b)凹曲线 (c)直线
由于A点在椭圆上,必满足式(1)的椭圆方程,即:
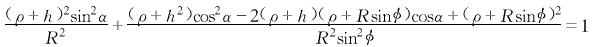
这是一个一元二次方程,可解出h:
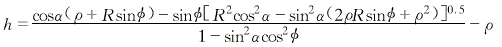 (12)
(12)
对于图4b,
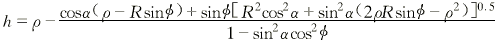 (13)
(13)
式(12)、(13)中
α=ΔSw/(2ρ) (14)
其中ΔSw为弧BC的弧长:
ΔSw=∫w2w1|r′(w,ui)|dw (15)
对于图4c,
h=Rsinφ-sinφ(R2-L2/4)0.5 (16)
此时,刀具的行距为线段L,即B、C两点间的距离。
至此,已经推导出了三种情形下残留高度的计算公式,可分别用式(12)、(13)、(16)计算出这三种情形下的残留高度。行距的大小就是根据h与ε的比较结果而定的。若h≤ε,那么此时的计算行距ΔSw就能满足要求;若h>ε,那么需要减小Δw,直至h≤ε为止。为求得满足条件的Δwmin,由步长算法可得到一组ui值,求出对应的Δw值,取其中的最小的Δw即为参数轴上的行距。
5 刀具轨迹的计算
刀具轨迹的计算包括刀具的中心点和刀具轴向矢量的计算。如图5所示,点A为刀具接触点,n为曲面在点A处的单位法矢量,Tax为刀具单位轴向矢量,Tc为由点A指向刀具中心的单位偏置矢量。
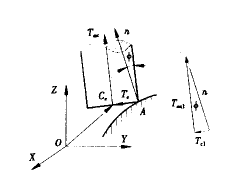
图5 刀具轨迹
因为n、Tax、Tc均在同一平面上,又Tc⊥Tax,那么矢量n、Tax1、Tc1组成一个矢量直角三角形。这里Tax1∥Tax,Tc1∥Tc,故:
Tc1=n-Tax1=n-|ncosφ|Tax
又cosφ=nTax,故:
Tc1=n-(nTax)Tax
单位化矢量Tc:
Tc=Tc1/|Tc1| (17)
其中刀具轴矢量Tax可将单位法矢量n在A点法平面内旋转φ角得到,即:
Tax=nTR (18)
上式中TR为旋转变换矩阵:
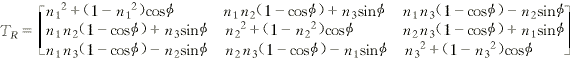
式中:n1、n2、n3——旋转轴单位矢量的方向余弦。
于是,刀具中心点的轨迹为:
Ce=r(w,u)+RTc (19)
6 结论
本文采用弦差法计算五轴立铣刀加工曲面的直线逼近误差,依据微分几何关系计算在最大直线逼近误差处刀轴摆动误差,由两者构成的加工误差来共同控制加工步长,该算法考虑了不同刀具接触点处的曲率差异。文中还对行距计算公式进行了推导,给出了刀位计算公式。该算法适合加工曲率变化大的曲面。