加工中心热误差补偿研究

热误差是机床最大的误差源之一。随着机械加工自动化和高精度化的发展，加工中心的热变形问题日益成为关注的焦点。

目前，减小机床热误差的研究可分为三类：(1)改进结构 设计和提高制造精度；(2)实现温度控制；(3)进行误 差建模和软件补偿。其中误差补偿技术，与前二者相比，具 有显著的有效性和经济性。尤其在我国，经济型数控机床众 多，通过误差补偿提高其热态下的加工精度具有重要的工程 应用前景。

本研究基于多体理论提出了热误差建模的理论和方法，对M AKINO加工中心的热误差进行了分析和辨识，并以实时 补偿方式进行了加工验证。

1 三轴加工中心热误差建模

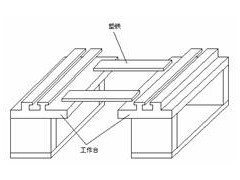
多体系统是对工程实际中复杂系统的高度概括。对于任何多 体系统都可用低序体阵列对系统拓扑结构进行数字化描述。这种描述方法为分析复杂多体系统提供了便利，并有助于建模的计算机化。图1为三轴MAKINO加工中心的结构示 意图。

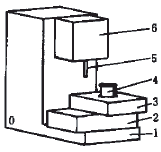
0.地基，惯性参考坐标系

1.床身 2.溜板 3.工作台

4.工件 5.刀具 6.主轴箱

图1 三轴加工中心结构示意图

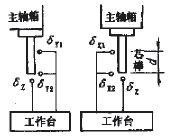
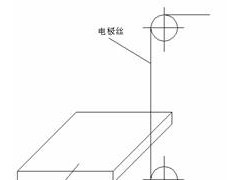
图2 五点测量法示意

热误差的测定

MAKINO加工中心具有良好的刚度和热结构。各驱动电 动机与床体分离，并具有高效的散热结构。在精加工条件下 ，主轴轴承摩擦是影响机床精度的主要热源，尤其高速旋转 时，主轴热伸长和漂移表现得更为突出。

本文采用5点法(如图2)测量主轴相对于工作台的热伸长、热倾斜和热漂移。测量仪器为电感测微仪，测量精度1µm。拾取机床温度装置为智能巡检仪，该仪器采用进口Pt-100热电阻元件，精确度达±0.15℃，并具有15个通道，可通过RS232标准通信接口由微机拾取温度信息。

根据MAKINO加工中心的结构特点(通过温升曲线分析和比较(去除相关性较大的温度测量点(并采用逐步回归分析法(最终确定了5个测量点的温度作为热误差参数辨识模型的输入，这5个测量点分别位于主轴轴端、立柱前侧上方、立柱后侧、床身，另一个用来监测环境温度。

热误差参数辨识

刀具相对于工作台的位置误差参数(用下标p表示)表现在e6px，e6py，e6pz，d6px，d 6py，d6pz六项热误差参数中，它们分别表示刀具(编号为6)相对于工作台在X、Y、Z三个方向上的角位置误差和线位置误差参数。由于e6pz对加工无影响，在此取值为零。所以通过五点法 完全可以确立其它五项参数，d6pz=dz，e6py= (dy2-dy1)/d，e6px=(dx1-dx2)/d，d6px=dx2+300×e6px，d6py=dy2-300×e6py；其中d代表同一侧两触头间的距离，芯棒有效长度为300mm；dx1、dx2、dy1、dy2、dz的含义见图2。实验中发现，由于加工中心结构对称、制造精度较高，主轴在X-Z平面内的热漂移和热倾斜、Y-Z平面内的热倾斜很小；在室温20℃、主轴转速800r/min、长达13h的转动下，X-Z平面内的热倾斜平衡在6.5×10-6rad(绝对值，不指示方向)，热漂移平衡在2µm，Y-Z平面内的热倾斜平衡在6×10-6rad，可见由主轴这几项热变形引起的误差量很小，对一般精度的数控机床而言，补偿意义不大，所以可令e6px，e6py，d6px为零。运用 多元线性回归方法对d6py，d6pz与5点温升间的关系进行拟合， 结果如下：

d6pz=0.3270-1.7336k[0]+12.5456k[1]-5.8040k[2]-6.7731k[3]-0.3 548k[4] (11)

d6py=0.6444+0.5304k[0]+5.1889k[1]-4.0763k[2]-2.9656k[3]+0.0741k[4] (12)

其中k[0]、k[1]、k[2]、k[3]、k[4]分别表示5个测温点采来的温度值。

2 热误差补偿实验验证

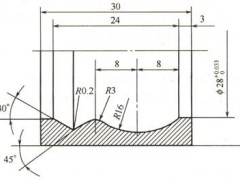
图3 实验样件示意

q

*:表示未经补偿加工的凸台 +:表示经补偿加工的凸台 -:表示理论值所在位置

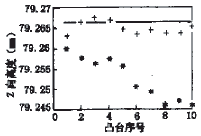
图5 凸台高度比较

样件设计及实验方案

考虑到实时补偿和验证模型的方便，整个试件如图3所示，基准面为底面和两个相邻的侧面。一天加工一行凸台(共10个)，两天的加工程序和环境温度情况尽可能一致；某一时刻只加工一个凸台的三个侧面，并在主轴以800r/min的速度空运转一定时间后，再接 着加工下一个凸台。凸台的尺寸为9mm×28mm×10mm，在一个凸台上耗费的加工时间在2min以内。

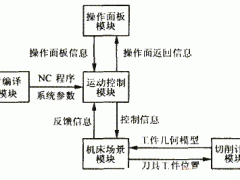
补偿加工时，在加工每个凸台前，微机实时拾取温度数据，通过补偿程序计算出误差量并修正加工程序；继而把修正后的加工程序迅速传输给加工中心，整个过程可控制在8s以内。因为机床的温升速度有限，所以可以认为这种补偿方法是实时的。补偿程序流程如图4所示。

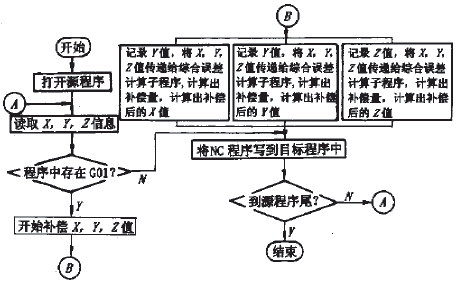
图4 补偿程序流程图

未经补偿和经补偿加工后的凸台高度比较

补偿结果试件经三坐标测量机测量后，将未经补偿的10个凸台与补偿加工后的10个凸台进行对比，结果显示补偿效果显著，精度提高平均在85%左右(见表和图5)。

3 结论

本文应用基于多体理论的误差分析理论和方法，建立了三轴加工中心的热误差模型，并结合MAKINO加工中心进行了热误差参数辨识和实验验证，取得了满意的补偿效果。研究结果证明，对于数控机床，通过该建模理论和相关的辨识方法，能既经济又显著地提高机床的加工精度，具有一定的推广和应用价值。