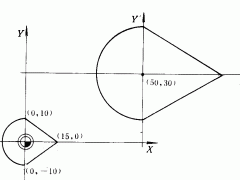
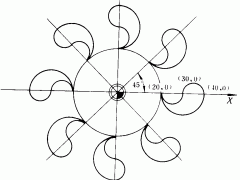
非圆曲线包括除圆以外的各种可以用方程描述的圆锥二次曲线(如:抛物线、椭圆、双曲线)、阿基米德螺线、对数螺旋线及各种参数方程、极坐标方程所描述的平面曲线与列表曲线等等。数控铣床在加工上述各种曲线平面轮廓时,一般都不能直接进行编程,而必须经过数学处理以后,以直线一圆弧逼近的方法来实现。但这一工作一般都比较复杂,有时靠手工处理已经不大可能,必须借助计算机作辅助处理,最好是采用计算机自动编程高级语言来编制加工程序。
处理用数学方程描述的平面非圆曲线轮廓图形,常采用相互连接的弦线逼近和圆弧逼近方法,下面将分别进行介绍。
1、弦线逼近法 一般来说,由于弦线法的插补节点均在曲线轮廓上,容易计算,程编也简便一些,所以常用弦线法来逼近非圆曲线,其缺点是插补误差较大,但只要处理得当还是可以满足加工需要的,关键在于插补段长度及插补误差控制。由于各种曲线上各点的曲率不同,如果要使各插补段长度均相等,则各段插补的误差大小不同。反之,如要使各段插补误差相同,则各插补段长度不等。下面是常用的两种处理方法。
1)等插补段法
等插补段法是使每个插补段长度相等,因而插补误差补等。编程时必须使产生的最大插补误差小于允差的1/2~1/3,以满足加工精度要求。一般都假设最大误差产生在曲线的曲率半径最小处,并沿曲线的法线方向计算,见图所示。这一假设虽然不够严格,但数控加工实践表明,对大多数情况是适用的。
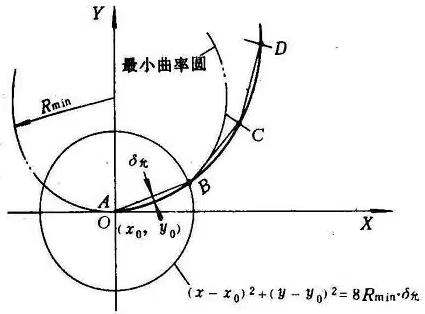
2)等插补误差法
等插补误差法是使各插补断的误差相等,并小于或等于允许的插补误差,这种确定插补段长度的方法称为“等插补误差法”。显然,按此法确定的各插补段长度是不等的,因此又叫“变步长法”。这种方法的优点是插补段数目比上述的“等插补段法”少。这对于一些大型和形状复杂的非圆曲线零件有较大意义。
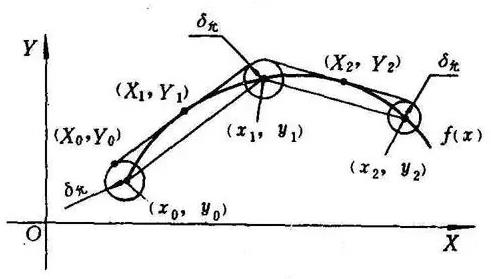
对于曲率变化较大的曲线,用此法求得的节点数最少,但计算稍繁。
2、圆弧逼近法
曲线的圆弧逼近有曲率圆法、三点圆法和相切圆法等方法。三点圆法是通过已知的三个节点求圆,并作为一个圆程序段。相切圆法是通过已知的四个节点分别作两个相切的圆,编出两个圆弧程序段。这两种方法都必须先用直线逼近方法求出各节点,再求出各圆,计算较繁琐。
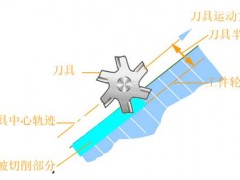
上面讲述的几种逼近计算中,只是计算了曲线轮廓的逼近线段或逼近圆弧段,还需应用等距线或等距圆的数学方法计算刀具中心的各节点坐标,作为编程数据。