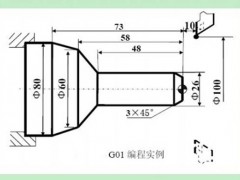
由于车削的毛坯多为棒料或铸、锻件,因此,车削加工多为大余量多次进刀切除,所以在车床的数控装置中,总是具备各种不同形式的固定循环功能,如内或外圆柱循环、内或外锥面循环、切槽循环、端面循环、内或外螺纹循环以及锥螺纹循环等等。应注意的是,不同国家、不同地区、不同公司的产品数控装置的这些循环指令代码及程序格式不尽完全相同,必须根据使用说明书具体规定进行编程,一般情况,对于数控车床大多采用G70~G79(为不指定代码)或G33~G35。以下仅对一些常用固定循环做一般性介绍。
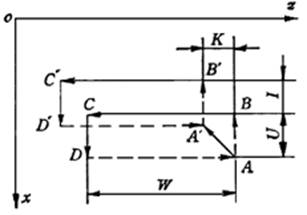

图1 内圆、外圆固定循环
1.车外圆、内圆固定循环指令:G⊿⊿
该指令用于内、外圆柱面切削的矩形自动循环。如图1,ABCD为一次自动循环,用一个循环指令并用一个程序段表示:
N-- G⊿⊿ X(U)-- Z(W)-- F-- LF
坐标值可用C点的增量值U、W,也可用C点的绝对坐标值X、Z。图示的U、W为负方向,U用AB的二倍值编程,并附上方向符号。图中虚线为G00快速,实线为程序中给定的F速度,但程序段中只编入F。
当进行重复循环时,为进一步减小程序,有些数控车床采用重复循环次数代码(如L或H代码)。设定每次循环完成后的推进量为I、K,则多次重复循环的动作可用一个程序段完成,即:
N-- G⊿⊿ X(U)-- Z(W)-- I-- K-- H-- F-- LF
H代码后的数字表示重复循环次数(包括第一次循环)。X(U)和Z(W)为第一次循环的坐标值。I用二倍值代入程序并附方向符号。
根据U、W、I、K的不同方向(正或负)可以组成不同切削方向的自动循环(如各种外圆或端面)。
2.锥度循环指令:G⊿⊿
用作切削内、外锥面的自动循环指令,如图2。锥度的斜率取决于U、W值。U值为圆锥大、小端直径差,编程时以二倍U值代入。当用绝对值编程时,取B点的X值与C点的Z值;当用增量值编程时,取AB之间的U值与AC之间的W值。车锥度大多应用增量坐标U、W编程。指令格式:
N-- G⊿⊿ X(U)-- Z(W)-- I-- K-- H-- F-- LF
式中I、K为A到A′的推进量,H为循环次数。
3.车简单螺纹循环:G⊿⊿
简单螺纹循环与圆柱循环基本相同,所不同的是F后边的进给量为螺纹导程值,单位为mm/r,并在切完螺纹的终点有斜向退刀动作CD。CD在Z向的距离约为一个导程。程序中的U值取大于螺纹牙深度二倍值以上编程;W值应包括切入和切出的空刀行程,如图4,即:
W = L + L1 + L2
L1和 L2为切入和切出的空刀行程,为保证加工出的螺纹质量,一般推荐:
L1为(3~5)F;L2为(1~2)F。
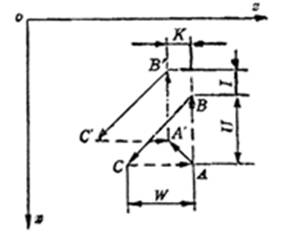
图2 锥度循环
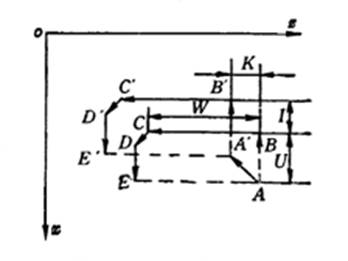
图3 简单螺纹循环
车削多头螺纹可用退刀的办法解决。如图5,以A点作为第一头螺纹的起点,当经过适当次循环后车好第一头螺纹后,把刀尖从A点退到G点作为第二头螺纹的起点,C点位置不变;依此类推,即可车削多头螺纹。设导程为F,螺纹头数为M,则每头的退刀距离为:H=F/M,并用H值编制退刀程序,这样就可以加工出多头螺纹。
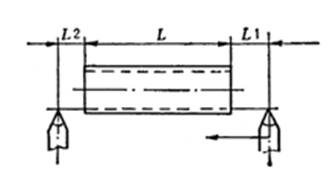
图4 螺纹行程
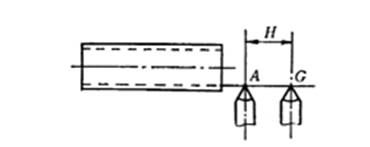
图5 多头螺纹的转换
锥螺纹循环基本上与图3所示柱螺纹循环相同,只是图中的BC段为螺纹的锥度(斜线)。
简单螺纹切削方式由于每次推进量I为固定值,即每次的切削剖面不等,是不合理的,不是理想的螺纹切削方式,所以称为简单螺纹循环。
4.复杂螺纹循环:G⊿⊿
复杂螺纹循环与简单螺纹循环相比,其主要特点是每次进刀深度是递减的,并且按一定规律由数控系统自动分配,其次是60°刀刃切入时,基本上是单侧切削。这些特点对大螺距加工是十分有利的。
复杂螺纹循环动作和程序格式有很多种,图6为其中一种循环方式的示意图,其程序段可写为:
N-- G⊿⊿ X— Z— I— D— F— A— LF
其中:G⊿⊿为该循环方式的指令代码;X、Z为C点的绝对坐标值;I为螺纹深度;D为第一次循环的切深;A为螺纹牙形角(如60°)。
螺纹深度I减去精加工余量a(0.1~0.6mm)为粗加工总余量。
粗加工余量 = I - a
每次粗切余量是递减的,递减规律决定于数控系统的内部程序。现举两种递减算法的例子:
1)如图6,当程序给定第一次粗切深D后,第二次及以后的每次总切深顺次为:
D1=D, D2=√D, D3=√D, D4=2D,……。
即每次的粗切深顺次为:D, D(√-1), D(√-√),D(2-√),……。
2)德国“西门子”3T系统,数控系统给定粗切次数n,则第一次粗切深为D:
D = 2(I-a)/(n+1)
每次的切深为:
D, D-d, D-2d, D-3d, ……。
其中:d=D/n, n为切削次数。
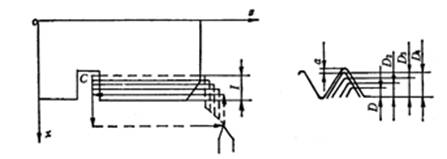
图6 复杂螺纹循环示意图
端面切削循环指令:G⊿⊿
如图7,用作端面切削固定循环,虚线表示快速移动(G00),实线表示指定的进给速度,刀具沿直线1234移动。指令格式为:
N-- G⊿⊿ X(U)-- Z(W)-- I-- K-- H-- F-- LF
式中符号同外圆、内圆固定循环。
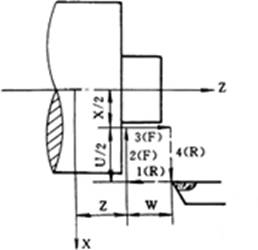
图7 端面循环