目前大多数全功能数控机床都具备刀具半径自动补偿G41、G42功能。这时,只要按工件轮廓尺寸编程,并输入刀具半径补偿值即可。但在机床数控系统不具备G41、G42指令的情况下,当用圆头车刀车削锥面及圆弧时,就不能按工件轮廓尺寸编程,而要经过复杂的补偿计算。也就是要计算假想刀尖轨迹或刀具中心轨迹并按计算出的轨迹编制程序。
(1)按假想刀尖编程及补偿计算
数控车床总是按刀尖对刀的。所谓假想刀尖如图1所示,图(b)为圆头刀具,P点为其假想刀尖,相当于图(a)理想尖头刀的刀尖点。
圆头车刀车削阶梯面
这时,无论是外圆、端面,或是内孔,假想刀尖轨迹与工件外形一致(工件尖角处除外),所以可以按工件轮廓尺寸编程,不需补偿计算。如图2。

1 圆头刀假想刀尖 图2 圆头刀加工台阶
圆头刀加工锥面
如图3(a),若假想刀尖P沿工件轮廓AB移动(即P1P2与AB重合),并按AB尺寸编程,则必然产生ABCD的残留误差。为此,应如图3(b)所示,使圆头刀的切削点移至AB,并沿AB移动,从而避免了残留误差。但这时假想刀尖的轨迹为P3P4,它与轮廓AB在X向相差⊿X,Z向相差⊿Z。设刀具半径为r,不难求得:
⊿X=r[2/(1 + ctg eq \o(\s\do-8(θ),\s\do 0(—),\s\do 8(2)))] ⊿Z=r(1 - tg eq \o(\s\do-8(θ),\s\do 0(—),\s\do 8(2)))
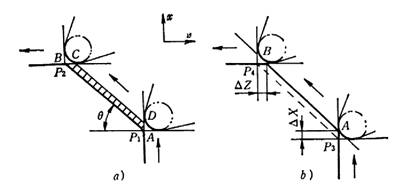
图3 圆头刀加工锥面
由于⊿X、⊿Z的存在,可直接按假想刀尖P3P4的坐标编程,即可切出轮廓AB。
圆头刀加工圆弧
圆头车刀加工圆弧表面的编程原理与加工锥面基本相似。图4为圆头刀加工1/4凹凸圆弧表面,AB(粗实线)为工件轮廓,半径为R,圆心O,刀具与圆弧轮廓起、终点的切削点分别为A和B,对应的假想刀尖为P1和P2。对图a凸圆加工情况,P1P2(虚线)为假想刀尖的轨迹,其半径为(R+r),圆心为O′。对图b凹圆情况同理,只是其半径为(R-r)。当用假想刀尖轨迹编程时,都按图中虚线所示的圆参数进行编程。
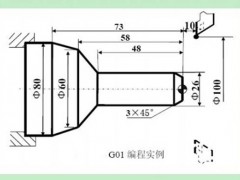
图5为圆头车刀加工圆弧、锥度的综合应用例。ABCDE为工件轮廓,BC圆弧的圆心为O,半径为R。各几何线型终点的假想刀尖点分别为P1(X1,Z1)、P2(X2,Z2)、P3(X3,Z3)。设刀具半径为r,则P1 P2假想刀尖圆的半径为(R+r),圆心为O′,其圆心坐标为I=0,K =-(R+r)。当用假想刀尖轨迹编程时,其程序为:
┇
G90 G01 X(X1) Z0 F-- LF
G03 X(X2) Z(Z2) I0 K-(R+r) LF
GO1 X(X3) Z(Z3)
┇
上述程序中的X1、Z1、X2、Z2、X3、Z3由简单的几何关系不难求得。
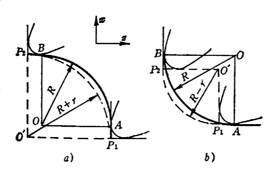

图4 圆头刀具加工90°凸凹圆 图5 用假象刀尖编制程序
(2)按刀心轨迹编程
如图6所示的零件,由三个圆弧组成,按刀心轨迹编程,用虚线所示的三段等距圆弧编程,即O1圆的半径为(R1+r),O2圆为(R2+r),O3圆为(R3-r),三个圆弧的终点坐标由等距圆的切点关系求得。用刀心轨迹方法编程比较直观,常被应用。
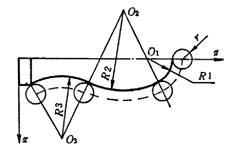
图6 刀心轨迹编程
上述用假想刀尖轨迹和刀心轨迹编程方法的共同缺点是当刀头磨损或刀具重磨后,需要重新计算编程参数并修改程序,否则,会产生误差。正因为此,现代的数控机床都具有G41、G42功能,刀具半径和刀具长度值可随时补偿修正。