在加工程序编制中,方法、技巧使用得当,对保证和提高数控机床的加工精度有重要的意义。笔者在长期的实践中,积累了一些编程经验,介绍如下。
1 消除公差带位置的影响
零件的许多尺寸标注有公差,且公差带的位置不可能一致,而数控程序一般按零件轮廓编制,即按零件的基本尺寸编制,忽略了公差带位置的影响。这样,即使数控机床的精度很高,加工出的零件也有可能不符合其尺寸公差要求。
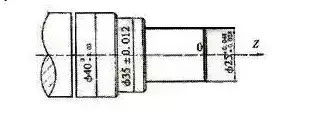
图1
如图1所示零件,?40尺寸为基轴制,?35尺寸为基孔制过渡配合,?25尺寸为基孔制过盈配合,3个尺寸的公差带位置不同,如果编程仍按其基本尺寸?40、?35与?25,而不考虑公差带位置的影响,就可能使某个尺寸加工不符合要求。解决问题的办法有2种:
1) 按基本尺寸编程,用半径补偿考虑公差带位置 即仍然按零件基本尺寸计算和编程,使用同一车刀加工各处外圆,而在加工不同公差带位置的尺寸时,采用不同的刀具半径补偿值。用这种方法,要先知道刀尖圆弧半径(此零件加工轨迹与X轴、Z轴平行,可不必知道刀尖圆弧半径),所以使用不便,且只能适用于部分数控系统。
2) 改变基本尺寸和公差带位置 即在保证零件极限尺寸不变的前提下,调整基本尺寸和公差带位置。一般按对称公差带调整,调整后的基本尺寸及公差如图2。编程时按调整后的基本尺寸进行,这样在精加工时用同一把车刀,相同的刀补值(本例加工轨迹与X轴、Z轴平行,可不刀补),就可保证加工精度。当然,如果零件最终还要精加工(如精磨),为保证磨削余量充裕,也可将基本尺寸稍稍加大(此时,公差带就不对称)。
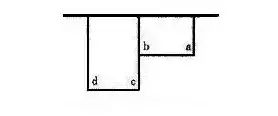
图2
2 消除机床间隙的影响
当数控机床长期使用或由于其本身传动系统结构上的原因,有可能存在反向死区误差。这时,可在数控编程和加工时采取一些措施,以消除反向死区误差,提高加工精度。尤其是当被加工的零件尺寸精度接近数控机床的重复定位精度时,更为重要。
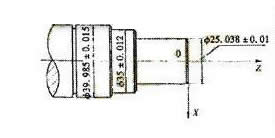
图3
1) 如图3所示,精加工工件轮廓为a→b→c→d,如采用如图4所示的刀具移动路线就不妥,因为从①→②的运动方向与③→④相反,会产生反向间隙,如改为图5所示的刀具移动路线,精加工时刀具在径向的移动保持尺寸连续递增趋势,在轴向的移动保持尺寸连续向左趋势,这样便消除了机床的反向间隙的影响。
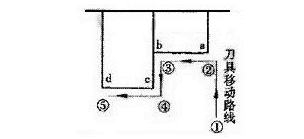
图4
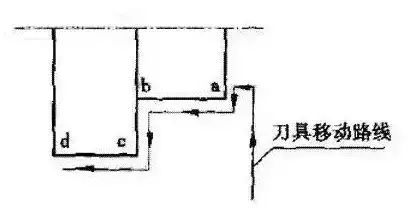
图5
2) 如图6所示,工件的①、②、③、④孔的孔距要求精确,设编程坐标系原点在工件中心点,对刀点(程序起点)也为同一点。如刀具移动路线为:原点O→①→②→③→④孔,则会产生反向间隙,如改为:原点O→A→①→②→③→④,即X方向和Y方向的尺寸保持连续递减或递增趋势,如保持连续递增和递减编程有困难.则应加过渡点,如图7中的B点,刀具移动为A→①→②→③→④,就可消除机床反向间隙。
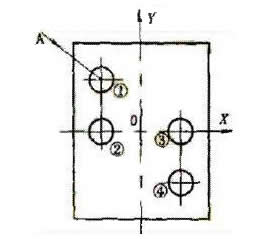
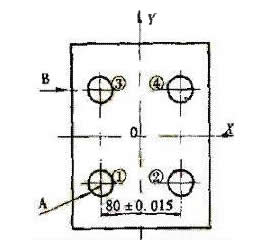
图6 图7
3 减小数控系统累积误差的影响
数控系统在进行快速移动和插补的运算过程中,会产生累积误差,当它达到一定值时,会使机床产生移动和定位误差,影响加工精度。以下措施可减小数控系统的累积误差。
尽量用绝对方式编程 绝对方式编程以某一固定点(工件坐标原点)为基准,每一段程序和整个加工过程都以此为基准。而增量方式编程,是以前一点为基准,连续执行多段程序必然产生累积误差。
插入回参考点指令 机床回参考点时,会使各坐标清零,这样便消除了数控系统运算的累积误差。在较长的程序中适当插入回参考点指令有益于保证加工精度。有换刀要求时,可回参考点换刀,这样一举两得


