公差设计与制造成本

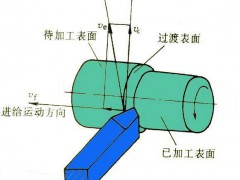
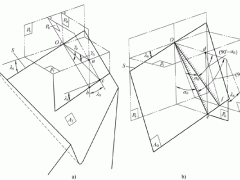
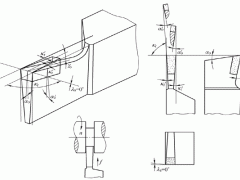
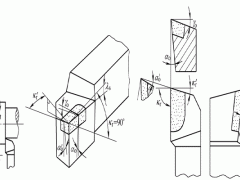
1 简介

公差设计应在使用要求及加工能力的约束下以成本最低作为目标函数。此成本应是包含了产品生命期中多项成本因素的综合的总成本，其中包括制造成本、质量损失成本、废次品损失成本、库存成本及机会损失成本等。制造成本是指产品在制造过程中发生的各种损耗的总和，是各种成本因素中最直接、最必不可少的成本因素。因此，对公差与制造成本进行建模是公差优化中的基础问题。

在很多情况下，设计师手中并未掌握有效的成本信息，其设计公差仅仅是从满足使用要求的角度来考虑的。任何设计均要通过制造过程来实现，在该过程中必然要造成成本损耗，而成本的多寡作为反馈信息将促使设计师调整其设计方案。通过多次实践调整最终达到以成本最低为目标的最优设计方案。显然，这种优化过程必然是以大量的成本浪费作为代价的。解决此问题的关键应在于使设计师掌握制造过程中的成本信息，使其在设计的同时就能进行基于成本的优化。对公差与制造成本的关系进行建模，即是为设计师提供此优化的依据。

虚拟制造要求对整个制造系统进行建模，使设计师在得出某一设计方案的同时就能拟合出实现该方案的整个制造过程，从而对设计方案进行评价和修改。并行工程要求在进行产品设计的同时，就要考虑其制造加工过程的可行性与成本问题。因此，对公差与制造成本关系进行建模，是符合先进制造的整体思想的，该模型也将成为虚拟制造与并行工程中的基础模型之一。

对设计公差与成本关系的建模方法应根据设计师所掌握的制造系统信息的不同而有所不同。在很多情况下，公差设计师不能获取制造系统的详细资料，不能确定设计公差所对应的工艺方法以及制造过程中的各种损耗，因此不能直接计算设计公差所对应的制造成本。但设计师能够获得一组经验公差—成本数据，即某些公差值所对应的成本数据。这些公差值是间断的，而设计师往往需要掌握各种精度范围内的公差—成本数据。也就是说，设计师需要掌握一条连续、完整的公差—成本关系曲线，而我们所已知的只是曲线上的一些离散点。此时即可利用曲线拟合法进行建模，在这些已知数据点的基础上拟合出一条完整的公差—成本曲线，从而为设计师提供任意精度范围内的公差—成本关系。

曲线拟合法即是将已有的公差—成本数据作依据，以某一曲线来对上述数据进行拟合，从而得到连续的公差—成本关系曲线，并以此作为今后设计的依据。应该指出，曲线拟合法是以某些公差—成本数据来推知其它公差所对应的成本，因此其基本假设是所有公差所对应的成本均是在同一制造系统中产生的，即制造系统的状态未发生改变。如制造系统状态发生了改变，根据已知的数据点是无法推测其它公差所对应的成本的。此时使用曲线拟合法必然带来较大的系统误差。

在此研究领域，Speckhart提出了指数模型，Spotts提出了倒数平方模型，Dong & Hu提出了多项式模型，S.H.Yeo等提出了自然样条模型。本文对以上传统的曲线拟合法进行了深入的研究对比，对公差—成本曲线进行了较详细的分析，在此基础上，提出了对公差—成本曲线进行分段拟合的建模方法。

2 公差—成本曲线

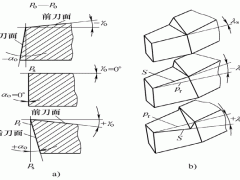
设计公差在制造系统中的实现总是通过一定的工艺序列完成的，如加工80h7轴的工艺序列为粗车—半精车—精车。一定的工艺序列有其一定的加工能力范围，当公差变化到一定程序时会引起工艺序列的变化，如粗车—半精车—粗磨—精磨。实验证明，同一工艺序列的公差—成本曲线与工艺序列变化时的曲线有不同的特征。

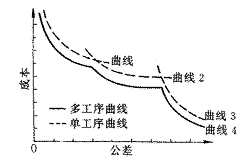
图1 公差成本曲线

考虑图1所示的公差—成本曲线，其中δ为公差，c为成本，可看作是公差的函数，记为c(δ)。同一工艺序列公差—成本曲线的特征可归纳如下：

曲线位于第一象限，且单调递减(不严格)

当δ→0时，c →+∞且c′(δ)→-∞

当δ→+∞时，c →B0(常数)且c′(δ)→0

曲线呈现凸函数曲线特征，无拐点

工艺序列变化时的公差—成本曲线是由多条同一工艺序列的曲线按照成本最低原则组合而成，其局部特点保留了同一工艺序列曲线的特征，曲线具有明显的分段性。

在设计师获取的经验数据中，特别是公差跨度范围较大的数据中，不同公差的实现往往采用了不同的工艺方法，因此我们拟合的对象应是工艺序列变化时的公差—成本曲线。

3 公差—成本曲线的分段拟合法

为了对经验成本—公差数据进行曲线拟合，Speckhart提出了指数模型，Spotts提出了倒数平方模型，Dong & Hu提出了多项式模型，S.H.Yeo等提出了自然样条模型。其中指数模型及倒数平方模型以及其它类似模型对数据点进行整体拟合，其曲线符合同一工艺序列公差—成本曲线的特征，即“合理”，但当数据组中包含工艺序列的变化时，在曲线中段的拟合精度不理想。多项式模型力图使拟合曲线在数据点上做到完全精确，但由于其振动问题(龙格现象)，使整体曲线不符合公差—成本曲线的基本特征，出现递增段，甚至出现成本负值，即曲线不合理。自然样条法假设相邻数据点间的曲线为三次多项式，且要求整个曲线的一阶、二阶导数连续，以至于出现与多项式模型同样的问题。因此，曲线拟合法的关键在于对数据点进行正确的分段，并在各段采用符合单工序曲线特征的函数来进行拟合。

对多工序公差—成本曲线进行拟合的首要问题在于对数据点的正确分段。利用单工序曲线的凸函数特征，本文提出了斜率判断法：设ki为数据点(xi,yi)与(xi+1,yi+1)间连线的斜率，应有ki≤0。如|ki|＜|ki+1|，则在xi与xi+1之间，曲线分段。

对分段后的曲线，可分别采用具有单工序曲线特征的函数进行拟合。考虑到指数模型能够合理地体现单工序曲线的特征，并且运用较为成熟，本文选用指数模型对各段曲线进行拟合。模型表达式为

c(δ)=a0+a1e-a2δ (1)

现举实例说明分段法的运用。下表为一组已知公差—成本数据。

分别计算相邻数据点连线的斜率为：-1.033、-0.62、0、-0.005、-0.056、0、0。根据斜率判断法，在数据点(8，1.24)与(16，1.20)之间进行分段。用指数模型进行拟合后，表达式与曲线如图2所示。

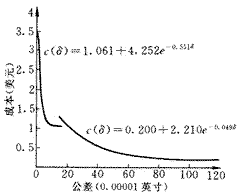
图2 多工序公差—成本曲线的分段拟合

分段曲线拟合法所得出的公差—成本曲线体现了产品加工的多工艺序列手段。曲线的分段体现了工艺序列的改变。在同一工艺序列，即同一段曲线上，制造成本随公差要求的提高而增加。每一工艺序列都具有一定的加工能力范围，即当公差要求增加到某一值，成本趋于无穷大。每一工艺序列都具有基本成本，公差要求降低到一定程序，成本不再降低，即曲线趋于水平。工艺序列变化的曲线是由多条同一工艺序列曲线以成本最低为原则组合而成的。值得注意的是，工艺序列变化曲线中的各段曲线可拓展成多条独立的同一工艺序列曲线，当系统出现特殊状态，如某一工序发生故障，即可寻找其他替代工艺序列，而这种替代将是以成本增加作为代价的。

工艺序列变化的公差—成本曲线不仅体现了成本随公差变化的整体趋势，同时也可反映出制造系统的加工水平。某国营中型企业近期进行了设备技术改造。原来主要加工方法为车削，主要加工工序为粗车—半精车—精车，随着零件使用要求的逐步提高，公差要求逐渐严格，精车工序须采用复杂精密卡具及高技术，有经验的工人才能达到要求，制造成本明显提高，而磨削工序由于机床数量少并且型号老化，开机成本较高，因此较少使用。经过设备技术改造，引进了一批新型磨床，并进行了人员培训同时制定了有效的管理方法，大大降低了磨削工序的使用成本。改进后工厂的主要工序转为粗车—半精车—粗磨—半精磨，大幅度提高了加工能力及质量。通过对该厂改造前后的公差—制造成本数据进行拟合，得出曲线如图3所示。可从以下几个方面对该图进行分析：

图3 制造系统改进前后的公差成本曲线

.在常用公差段内，曲线2在曲线1的下方，即实现相同公差值，改造后的制造系统所耗费的成本较少，从而体现了改造后系统的生产及管理水平高于改造前。

曲线2在曲线1的左方，即改造后系统的加工能力范围大于改造前系统，体现了系统技术水平的提高。

曲线2中磨削加工与车削加工的交点比曲线1靠右，表明改造后系统更加大范围地使用较高水平的加工方法，即高水平的加工方法更加成熟。

通过对公差—制造成本曲线的分析可得出，改造后制造系统的整体水平优于改造前。

4 结论

运用曲线拟合法进行优化设计，可避免由实际制造的成本过高而修改设计造成的损失，同时也大大缩短了设计周期，提高了设计的灵敏度。采用曲线拟合法得出的公差—制造成本曲线，还反映了制造系统的整体信息，对公差—制造成本曲线进行分析和比较，可对制造系统的加工能力及管理水平进行评价。因此，运用曲线拟合法对公差与制造成本的关系进行建模，符合先进制造的整体思想，是公差优化中的基础理论依据。