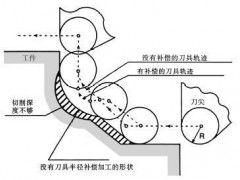
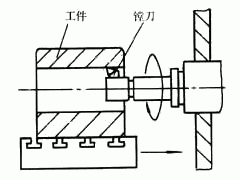
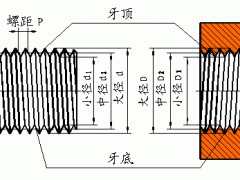
在机械加工过程中,常利用尺寸链原理求解工序尺寸及其公差。但当零件加工工序较多,工艺基准与设计基准又不重合,加工中又需多次转换定位基准时,想快速、准确的建立起尺寸链并非易事。此时,人们大多会利用“图解法”。由于传统图解法中工序尺寸的表示及加工余量的位置均没有按实际加工状况画,造成工序尺寸概念不清和各尺寸间关系混乱,给尺寸链的建立带来了一定困难。本文针对传统图解法存在的问题,推出了一种直观明了、真实反应加工过程各尺寸联系的“简明工序尺寸图解法”,现结合实例介绍如下。
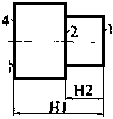
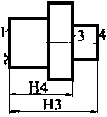
(a)工序05 (b)工序10
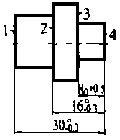
图1 零件简图 图2 工序图
例:某零件简图如图1所示,其机械加工工艺过程由工序05(图2a)和工序10(图2b)组成,试求工序尺寸H1,H2,H3,H4及其极限偏差。(注:各表面机械加工余量均为1.5m )
1 用简明的工序尺寸图解法建立工艺尺寸链的步骤
准备工作
徒手画出零件简图,在简图上方标出设计尺寸。(如图3)
分析零件加工过程,了解各表面加工次数。本例中,表面1,2,3,4各加工一次。
在零件图各加工表面加上余量,将零件图转化为毛坯草图。
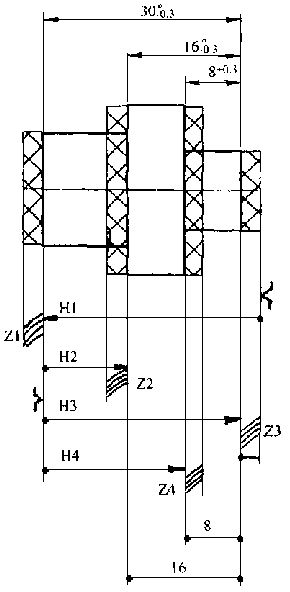
注意:a.每个表面加工几次就应加上几层余量:b.为使图解清楚,余量应适当放大。
本零件图转化后的手坏草图如图3所示。
用图解表示加工过程
从将要加工的各表面向下引竖线,分别代表毛坯表面和各工序加工表面。
严格按照加工顺序,从上到下,用规定符号表示加工过程。
如用表示定位基准,用“·”表示工序基准,用表示加工表面,用表示工序尺寸,用表示加工余量等。
本例的图解建立如图3所示。
注意:图解中工序基准、工序尺寸、加工余量等必须按实际加工位置画,箭头应指向各工序已加工表面。
本步骤用规定的符号将整个加工过程的不同工序“集合”于同一张图上,直观、清楚地表示出了零件在由毛坯变为成品过程中,各加工表面尺寸真实的变化情况以及各尺寸之间的内在联系,形成了工艺过程“尺寸联系图”。这是建立工艺尺寸链的关键之处,务必小心。
由图解建立尺寸链
确定封闭环
机械加工工艺过程中的封闭环有两类。
间接得到的设计尺寸为封闭环。
加工余量(靠火花磨削除外)为封闭环。
由于封闭环必定是间接形成的,故可将封闭环画在整个图解的最下方,用表示。本例中,设计尺寸30-0.3直接得到的,是组成环;而设计尺寸8+0.3和16-0.3是间接得到的,是封闭环;余量Z1,Z2、Z3,Z4均是封闭环。
由封闭环查找组成环
由上述得到的一个个封闭环,依次查找相关的组成环,以形成尺寸链。
查找组成环时可依如下口诀进行:
从封闭环两端向上找,遇到箭头拐弯找,遇到“·”继续向上找。直到相交。
说明:
遇到箭头意味着此工序尺寸对封闭环有影响,应计人尺寸链中,故应拐弯;遇到“·”意味着仍为同一基准,故应继续向上,而不能拐弯。
一个封闭环只能建立一个尺寸链,而一个尺寸链只能求解一个未知量,故除直接得到的工序尺寸外,有多少个未知量,就应建立多少个尺寸链。
将查找出的尺寸链单独列出,形成尺寸链图。
本例中形成的与工序尺寸有关的尺寸链图如图4(a),(b),(c)所示。
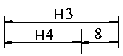
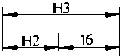
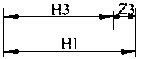
(a) (b) (c)
图4 尺寸链图
2 工艺尺寸链的解算
建立工艺尺寸链的目的在于求解工序尺寸及其公差、验算加工余量的大小,利用尺寸链计算公式即可求解。但需注意以下几个问题:
组成环公差超差时的处理
计算尺寸链时,有时会出现组成环公差之和大于封闭环公差的情况,这是不允许的。此时,应提高相应工序的加工精度,压缩组成环的公差。
本例中,尺寸H3=300.3是直接得到的设计尺寸,由于其公差己等于封闭环8+0.3和16-0.3的公差,故应将其压缩。本例取H3=30-0.15,求得H2=14+0.15, H4=22-0.15-0.30。
公共组成环的处理
公共组成环应同时满足其所在的多个尺寸链对其公差与偏差要求,应由对其精度要求高的尺寸链来决定其公差与偏差。
协调环的处理
当一个尺寸链中有多个未知工序尺寸时,需选取一个组成环作为协调环,它的极限偏差不能事先确定,而只能在其它各环极限偏差已确定的情况下,通过尺寸链计算确定,以满足封闭环极限偏差的要求。
与设计尺寸无关的组成环的处理
与设计尺寸无关的尺寸,其公差可按本加工工序的经济精度等级确定,偏差可采用入体原则标注。
本例中,尺寸H1与设计尺寸无直接关系,其基本尺寸H1=H3+Z3=31. 5mm,取经济精度等级为IT12,公差T=0.25mm,偏差按入体原则标注,则H1=31.5-0.25mm。
3 结束语
本图解法中,工序尺寸及余量的表示与实际加工状况完全一致,非常直观,便于推广。
建立图解、确定封闭环、查找组成环是建立尺寸链的三部曲。建立图解的本质是用“规定符号”表示加工过程;确定封闭环的关键是找出“间接获得”的设计尺寸;而牢记文中“口诀”,则可快速地找到组成环,继而建立起尺寸链。
本图解法适用于任何复杂的工艺尺寸链建立,效率高,效果好,极具推广和实用价值。