第三节 数据采样法插补原理实验
一、实验目的
1.掌握数据采样法直线与圆弧插补的基本原理
2.了解数据采样法直线插补与圆弧插补的程序编制方法
3.加深对数据采样法插补的理解
二、实验原理
随着数控系统中计算机的引入,插补实时性和计算复杂性之间的矛盾已不再那么突出了。因此,现代数控系统中就采用了结合计算机采样思想的数据采样插补法。
数据采样法实际上是一种粗插补过程,它所产生的微小线段仍然比较大,必须进一步对其密化(即精插补)。粗插补算法较复杂,大多用高级语言编制;精插补算法较简单,多用汇编语言或硬件插补器实现。
粗插补产生微小线段的周期称为插补周期Ts,精插补的周期称为位置控制周期Tc,它是伺服位置环的采样控制周期。对于特定的系统,Ts、Tc是两个固定不变的时间参数,且Ts=nTc,n为自然数。
Ts对系统稳定性没有影响,但对被加工轮廓的轨迹精度有影响,Ts愈大,则产生的微小线段愈长(△L=FTs,F为程编速度),插补计算误差就愈大。而Tc对系统稳定性和被加工轮廓的轨迹精度都有影响。
可见,为减小插补误差,应尽量减小Ts,但Ts若太小,则CPU可能来不及进行位置计算、显示、监控、I/O处理等CNC任务,Ts必须大于插补运行时间和完成其他相关
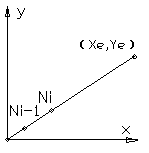
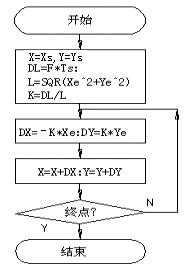
图4-18 第一象限直线 图4-19 第一象限数据采样直线插补软件流程图
任务所需时间之和。目前,Ts一般在10ms左右,如美国AB公司的7360CNC系统,Ts=10.24ms;德国SIEMENS公司的System-7CNC系统,Ts=8ms。随着计算机速度的提高,Ts有减小的趋势。
Tc选择一般有两种情况:Tc=Ts(7360CNC系统),Tc=0.5Ts(System-7CNC系统)。
以上是数据采样法的基本原理,下面讨论插补具体轮廓线时的情形。
1.1. 直线插补
图4-18为第一象限直线,现分析其插补规律。
刀尖从点Ni-1移动到点Ni,沿轮廓直线方向的增量为DL=F×Ts,沿X向的增量为DX,沿Y向的增量为DY,它们之间的关系是:
DX=DL×Xe/L,DY=DL×Ye/L
其中,L为轮廓直线的长度,它满足等式:L2=Xe2+Ye2
Ni点的动态坐标可以用前一个点的坐标动态表示:X=X+DX,Y=Y+DY
由此,可设计第一象限数据采样直线插补软件流程图,见图4-19。
2.2. 圆弧插补
数据采样法圆弧插补的基本思路是在满足加工精度的前提下,用切线、弦线或割线来代替圆弧实现进给,即用直线逼近圆弧。
(1)切线法(一阶DDA算法)
图4-20为第一象限逆圆,现分析其切线法插补规律。
设当前点在Ni-1,按切线方向前进一个粗插补周期后到达Ni点,走过的粗插补
单位长度为 L=F×Ts,其中:F为进给速度,粗插补周期为Ts。
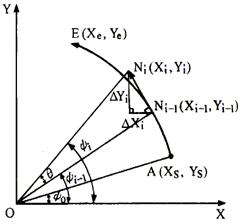
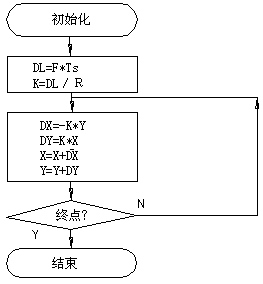
图4-20 切线法逆圆插补示意图 图4-21切线法圆弧插补流程图
显然,Xi-1=Rcosψi-1 (R为圆弧半径)
Yi-1=Rsinψi-1
Xi=Rcos(ψi-1+θ)
Yi=Rsin(ψi-1+θ)
从而
Xi=Xi-1cosθ-Yi-1 sinθ
Yi=Yi-1cosθ+Xi-1 sinθ
因θ很小,所以
sinθ=θ-θ3/3!+θ5/5!-……
cosθ=1-θ2/2!+θ4/4!-……
取一阶近似(一阶DDA名称的由来),得
sinθ=θ=F×Ts/R=K
cosθ=1
因此
Xi=Xi-1-KYi-1
Yi=Yi-1+KXi-1
![]() Xi=Xi-Xi-1=-KYi-1
Xi=Xi-Xi-1=-KYi-1
![]() Yi=Yi-Yi-1=KXi-1
Yi=Yi-Yi-1=KXi-1
由此,可设计第一象限切线法数据采样圆弧插补软件流程图,见图4-21。
本法与脉冲增量方式DDA插补在本质上是相同的,前者是后者的推广。由于误差太大(可以在随后的实验中验证),在实际的CNC系统中并不使用。
(2)弦线法(直接函数算法)
图4-22为第一象限顺圆,弦线法插补规律(请参考有关书籍自行分析)如下:
Ⅰ区:
∆Xi=(Yi-1+∆Yi-1×0.5)×FTs/R
∆Yi=-Yi-1+(R2-(Xi-1+∆Xi)2)1/2
Xi=Xi-1+∆Xi
Yi=Yi-1+∆Yi
Ⅱ区:
∆Yi=(Xi-1+∆Xi-1×0.5)×FTs/R
∆Xi=-Xi-1+(R2-(Yi-1+∆Yi)2)1/2
Xi=Xi-1+∆Xi
Yi=Yi-1+∆Yi
Ⅲ区:
∆Xi=(Yi-1+∆Yi-1×0.5)×FTs/R#8710;Yi=-Yi-1—(R2-(Xi-1+∆Xi)2)1/2
Xi=Xi-1+∆Xi
Yi=Yi-1+∆Yi
Ⅳ区:
∆Yi=(Xi-1+∆Xi-1×0.5)×FTs/R
∆Xi=-Xi-1-(R2-(Yi-1+∆Yi)2)1/2
Xi=Xi-1+∆Xi
Yi=Yi-1+∆Yi
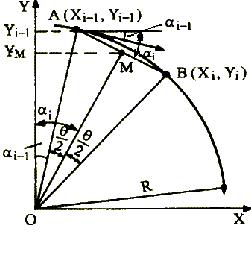
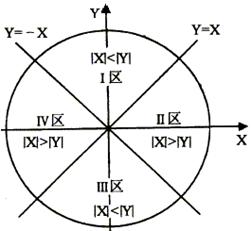
图4-22 弦线法顺圆插补示意图 图4-23 分区图
分区情况见图4-23。由此,不难得到其流程图4-24。
弦线法的精度比切线法高。
(3)割线法(二阶DDA算法)
一阶算法时曾得到:sinθ=θ-θ3/3!+θ5/5!-……
cosθ=1-θ2/2!+θ4/4!-……
我们现在取两阶近似,即为二阶DDA算法:
sinθ=θ-θ3/3!≈θ
cosθ=1-θ2/2!≈1-0.5×θ2
图4-25逆圆第一象限插补时,可计算得到:
∆Xi=K×Yi-1-0.5×Xi-1K2
∆Yi=-K×Xi-1-0.5×Yi-1K2
Xi=Xi-1+∆Xi
Yi=Yi-1+∆Yi
按此编制程序流程图4-26。割线法的精度比弦线法高。
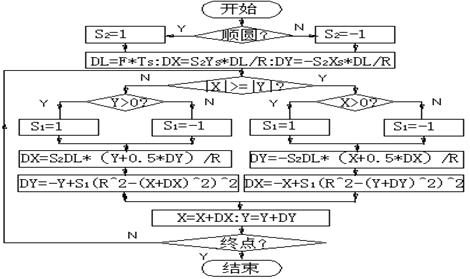
图4-24 弦线法圆弧插补流程图
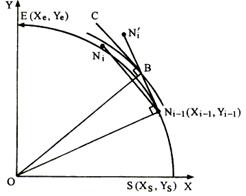
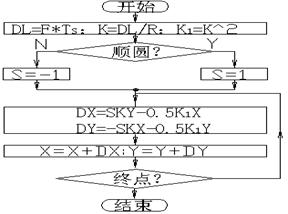
图4-25 割线法逆圆插补示意图 图4-26 割线法圆弧插补流程图
3.参考程序:
直线:
Sub 插补()
Dim l, K, a, B, f1, t
x动点对起点 = 0: z动点对起点 = 0
f1 = f × 10: t = Ts / 60000
l = Sqr((x终点对起点 ^ 2 + z终点对起点 ^ 2))
K = f1 × t / l
a = Sqr((x动点对起点 - x终点对起点) ^ 2 + (z动点对起点 - z终点对起点) ^ 2)
x步长 = K × x终点对起点: z步长 = K × z终点对起点:
B = Sqr(z步长 ^ 2 + x步长 ^ 2)
Do Until a <= B / 2
x动点对起点 = x动点对起点 + x步长: z动点对起点 = z动点对起点 + z步长
a = Sqr((x动点对起点 - x终点对起点) ^ 2 + (z动点对起点 - z终点对起点) ^ 2)
Line -Step(z步长 × 系数, x步长 × 系数), vbRed
x动点对原点 = x动点对起点 + x起点对原点: y动点对原点 = y动点对起点 + y起点对原点: z动点对原点 = z动点对起点 + z起点对原点
Loop
End Sub
圆弧(切线法):
Sub 插补()
Dim 区间符号 As Integer
Dim x, y, z As Double
Dim K
Dim 径向误差, R动 As Double
顺逆符号判别
读数据
If R < 0.001 Then
Else
Ts = Ts / 60000
步长 = f × Ts:
K = 步长 / R
x动点对圆心 = -x圆心对起点 / 系数: z动点对圆心 = -z圆心对起点 / 系数
End If
x = ((x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2) ^ 0.5
y = 3 × 步长 × 系数
Do Until x <= y
deltaZ = -顺逆符号 × K × x动点对圆心
deltaX = 顺逆符号 × K × z动点对圆心
Line -Step(deltaZ, deltaX), vbRed
x动点对圆心 = x动点对圆心 + deltaX: z动点对圆心 = z动点对圆心 + deltaZ:
x动点对原点 = x动点对圆心 + x圆心对原点: y动点对原点 = y动点对圆心 + y圆心对原点: z动点对原点 = z动点对圆心 + z圆心对原点:
x = ((x动点对圆心 - x终点对圆心) ^ 2 + (z动点对圆心 - z终点对圆心) ^ 2) ^ 0.5:
y = 3 × 步长 × 系数
R动 = Sqr(x动点对圆心 ^ 2 + z动点对圆心 ^ 2)
Loop
End Sub