B样条曲线和后面的B样条曲面法在数控加工中得到了广泛的应用，它的特点是几何性质好、计算程序简单、计算速度快。列表曲线采用B样条拟合时，是用许多B样条曲线段近似列表轮廓曲线，然后再用许多小直线段（或圆弧段）代替B样条曲线段来组成所要求的轮廓形状。下面简单介绍B样条曲线算法。
图1（a）表示一段三次B样条曲线，它由特征多边形四个顶点Vi、Vi+1、Vi+2和Vi+3构成。B样条曲线段的起点ri （0）落在DVi Vi+1 Vi+2的中线Vi+1m上距Vi+1的1/3处。起点的切矢ri （0）平行于DVi Vi+1 Vi+2的底边，长度为其一半。起点的二阶导矢量ri ²（0）等于中线向量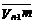 
的二倍。终点的情况同起点相对称。这样就大体上确定了一个B样条曲线段的形状。
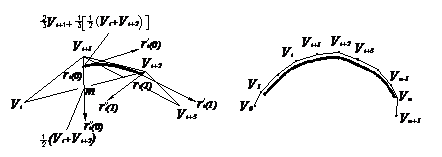
（a） （b）
图1 三次B样条曲线段和曲线
当特征多边形的顶点超过四点时，每增加一个顶点，则相应的样条上增加一段曲线。图1（b）表示出特征多边形及其对应的B样条曲线。如果希望B样条曲线要通过首末顶点，则可采用三重节点法，即在首末节点处取重复节点，或采用三顶点共线法。
三次B样条曲线公式为
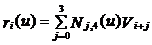
（8）
式中，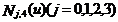 
为三次B样条基函数，分别为参数u（0£ u £1）的三次多项式，即
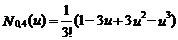
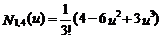
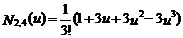
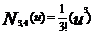
由式（8）得
（9）
特征多边形顶点Vi+j和三次B样条基函数Nj,4（u）线性组合得到ri（u）。当参数u从0变化到1时，上式就描绘出第i段曲线。各段曲线在连接点处保持C2阶连续。
用上述方法得到的B样条虽然接近列表点，但并不通过列表点。在列表曲线处理中我们希望用B样条曲线来拟合给定列表点（即型值点），然后再求插值点。因此需要先根据型值点计算出特征多边形顶点位置矢量{Vi}（i= -１，0，1，…，n+1），即“反算”，再对曲线进行插值计算。
已知n+1个型值点Pi（xi，yi）（i=0，1，2，…，n），从式（9）中第一、第二式可看出，顶点的求解可归结为下列线性代数方程组的求解：
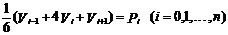
（10）
由于式（10）方程组有n+3个未知数，而方程只有n+1个，故必须根据端点条件补充两个方程，端点条件有多种给法，这里仅给出一种两端点切矢量的方法，即
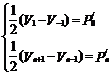
（11）
将式（11）分别与式（10）联立，消去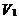 
和 
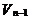得
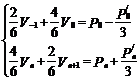
（12）
用追赶法可求解由式（12）和式（10）构成的三对角线性方程组，即可求得特征多边形各顶点位置矢量。
将求得的特征多边形顶点位置矢量{Vi}代入公式（8）中，取不同的u值可得曲线上各插值点坐标。
