以第Ⅰ象限逆圆为例,设刀具沿圆弧![]() 移动,半径为R,刀具的切向速度为v, P(x,y) 为动点(如图2—13),
移动,半径为R,刀具的切向速度为v, P(x,y) 为动点(如图2—13),

图2-13 DDA圆弧插补
则有下述关系:
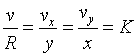
式中K为比例常数。因为半径R为常数,切向速度V为匀速,所以K可认为是常数。
在单位时间增量Δt内,x和 y位移增量的参量方程可表示为
![]() (2—10)
(2—10)
![]() (2—11)
(2—11)
根据此两式,仿照直线插补方案用两个积分器来实现圆弧插补,如图2—14(a)所示。图中系数K的省略原因和直线时类同。但必须指出:第一,坐标值 x和 y存入寄存器Jvx和Jvy的对应关系与直线不同,恰好位置互调,即 y存入Jvx,而x存入Jvy中。第二,Jvx和Jvy寄存器中寄存的数值与直线插补时还有一个本质的区别:直线插补时Jvx(或Jvy)寄存的是终点坐标xe(或ye),是个常数;而在圆弧插补时寄存的是动点坐标,是个变量。因此在刀具移动过程中必须根据刀具位置的变化来更改速度寄存器Jvx和Jvy中的内容。在起点时,Jvx和Jvy分别寄存起点坐标值y0和x0;在插补过程中,JRy每溢出一个 Δy脉冲,Jvx寄存器应该加“1”;反之,当JRx溢出一个 Δx脉冲时,Jvy应该减“1”。减“1”的原因是刀具在作逆圆运动时 x坐标须作负方向进给,动坐标不断减少。图2—14中用⊕及Ө表示修改动点坐标时这种加“1”或减“1”的关系。图2—14(b)为第Ⅰ象限逆时针走向的圆弧插补的数字积分器符号表示图。
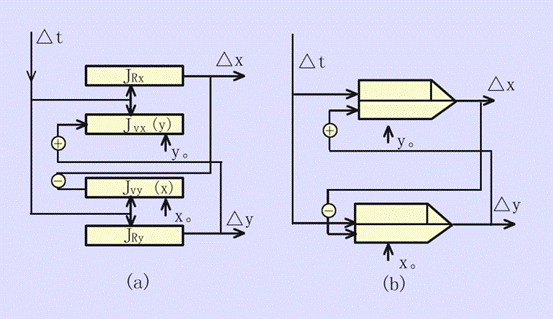
图2-14 DDA圆弧插补运算框图及符号图
对于顺圆、逆圆及其他象限的插补运算过程和积分器结构基本上与第Ⅰ象限逆圆是一致的。其不同在于,控制各坐标轴的Δx 和 Δy的进给方向不同,以及修改Jvx和Jvy内容时是⊕还是Ө,要由 y和 x坐标的增减而定,见表2—5。
表2-5 DDA圆弧插补时的坐标修改情况见图2—15。
| SR1 | SR2 | SR3 | SR4 | NR1 | NR2 | NR3 | NR4 | |
| Jvx(y) | 一 | + | 一 | + | + | 一 | + | 一 |
| Jvy(x) | + | 一 | + | 一 | 一 | 一 | + | + |
| ∆x | + | + | - | - | - | - | + | + |
| ∆y | - | + | + | - | + | - | - | + |
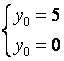 和
和 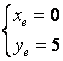 DDA圆弧插补的终点判别可以利用两个终点减法计数器,把 x和 y坐标所需输出的脉冲数| xe-x0|和| ye-y0|分别存入这两个计数器中, x或 y积分器每输出一个脉冲,相应的减法计数器减1,当某一坐标计数器为零时,说明该坐标已到达终点,这时,该坐标停止迭代。当两个计数器均为零时,圆弧插补结束。下面举一个DDA圆弧插补的具体例子。设有一个圆弧,起点为 A(5,0),终点为 B(0,5),即
DDA圆弧插补的终点判别可以利用两个终点减法计数器,把 x和 y坐标所需输出的脉冲数| xe-x0|和| ye-y0|分别存入这两个计数器中, x或 y积分器每输出一个脉冲,相应的减法计数器减1,当某一坐标计数器为零时,说明该坐标已到达终点,这时,该坐标停止迭代。当两个计数器均为零时,圆弧插补结束。下面举一个DDA圆弧插补的具体例子。设有一个圆弧,起点为 A(5,0),终点为 B(0,5),即

图2-15 DDA圆弧插补轨迹
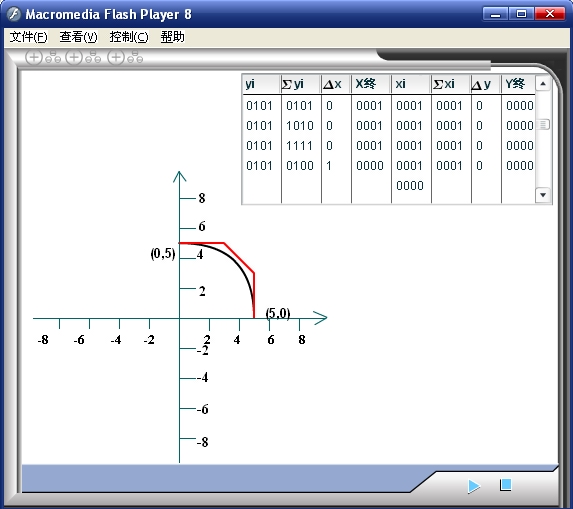
图2-16 DDA圆弧插补过程
