由高等数学可知,求函数y =f(t)对t的积分运算,从几何概念上讲,就是求此函数曲线 所包围的面积 F(图2—7),即


若把自变量的积分区间[a,b]等分成许多有限的小区间![]() (其中
(其中 ![]() ),这样,求面积可以转化成求有限个小区间面积之和,即
),这样,求面积可以转化成求有限个小区间面积之和,即

数字运算时,Δt一般取最小单位“1”,即一个脉冲当量,则
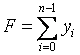
由此可见,函数的积分运算变成了变量的求和运算。当所选取的积分间隔Δt足够小时,
则用求和运算代替求积运算所引起的误差可以不超过允许的值。
由高等数学可知,求函数y =f(t)对t的积分运算,从几何概念上讲,就是求此函数曲线 所包围的面积 F(图2—7),即


若把自变量的积分区间[a,b]等分成许多有限的小区间![]() (其中
(其中 ![]() ),这样,求面积可以转化成求有限个小区间面积之和,即
),这样,求面积可以转化成求有限个小区间面积之和,即

数字运算时,Δt一般取最小单位“1”,即一个脉冲当量,则
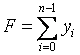
由此可见,函数的积分运算变成了变量的求和运算。当所选取的积分间隔Δt足够小时,
则用求和运算代替求积运算所引起的误差可以不超过允许的值。
版权声明:本站部分内容文章及图片来自互联网或自媒体,版权归属于原作者。如内容、图片有任何版权侵权问题,请联系我们处理,我们将在第一时间删除内容。
免责声明:数控信息网发布此文目的在于促进信息交流,不存在盈利性目的,此文观点与本站立场无关,不承担任何责任。未经证实的信息仅供参考,据此操作风险自担。如遇虚假诈骗信息,请立即举报
0评论2023-05-30478
0评论2023-05-30539
0评论2023-05-29335
0评论2023-05-29451
0评论2023-05-29355
0评论2023-05-29538
0评论2023-05-29432
0评论2023-05-29363
0评论2023-05-29511