如图2－29所示，顺圆弧AB为待加工曲线，下面推导其插补公式。在顺圆弧上的B点是继A点之后的插补瞬时点，两点的坐标分别为A(xi,yi)，B(xi+1,yi+1)。所谓插补，在这里是指由点A(xi,yi)求出下一点B(xi+1,yi+1) ，实质上是求在一次插补周期的时间内，x轴和y轴的进给量Δx和Δy。图中的弦AB正是圆弧插补时每个周期的进给步长ƒ，AP是A点的圆弧切线，M是弦的中点。显然，ME⊥AF，E是AF的中点，而OM⊥AB。由此，圆心角具有下列关系：

                                   （2-19）

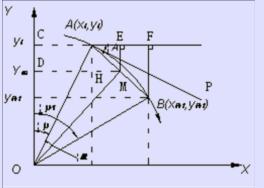
图2-29时间分割法圆弧插补

式中δ为进给步长ƒ所对应的角增量，称为角步距。由于       ΔAOC～ΔPAF

所以

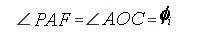
显然

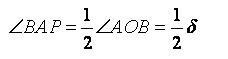
因此

在△MOD中       

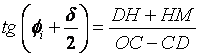
将     

                   =        ；        =       ；

代入上式，则有

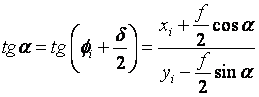                               （2-20）

因为      

而                          

             ;  

又可以推出xi和yi，Δx和Δy的关系式：

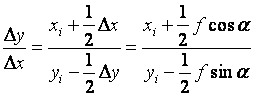                              （2-21）

上式充分反映了圆弧上任意相邻两点的坐标间的关系。只要找到计算Δx和Δy 的恰当方法，就可以按下式求出新的插补点坐标：

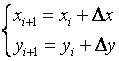                                      （2-22）

所以，关键是求解出Δx和Δy。事实上，只要求出tgα 值，根据函数关系便可求得Δx，Δy值，进而求得xi+1，yi+1值。

由于式（2-20）中的sinα和cosα均为未知数，要直接算出tgα 很困难。7M系统采用的是一种近似算法，即以cos45°和sin45°来代替cosα 和sinα ，先求出

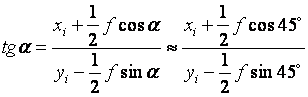                       （2-23）

再由关系式

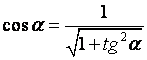                                 （2-24）

进而求得

                               （2-25）

由式（2-23）、（2-24）、（2-25）求出本周期的位移增量Δx后，将其与已知的坐标值xi，yi代入式（2-21），即可求得Δy值。在这种算法中，以弦进给代替弧进给是造成径向误差的主要原因。